مساحت مستطیل چگونه بدست می‌آید؟ ریاضی پایه ششم

برای محاسبه محیط و مساحت شکل هندسی مستطیل باید با فرمول های مربوطه و نحوه محاسبه این چهار ضلعی آشنا باشید. مستطیل از اشکال هندسی پر کاربرد است، با این وجود شکل مستطیل نوعی مربع است با این تفاوت که از 4 ضلع آن، 2 ضلع طول بیشتری نسبت به دو ضلع دیگر دارند و از طرفی از 4 اضلاع، 2 به 2 با یکدیگر موازی و در یک راستا قرار دارند.

محاسبه مساحت مستطیل

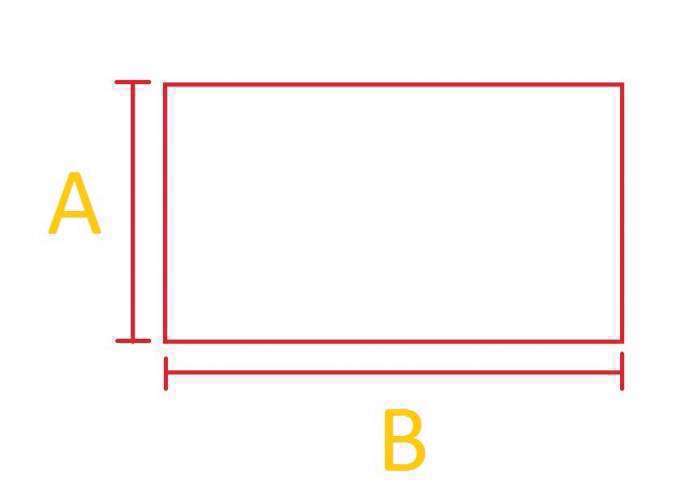
برای محاسبه مساحت مستطیل نیز شما نیاز به محاسبه طول و عرض مستطیل دارید و بعد از این طول و عرض را بدست آوردید، آنها را با یک دیگر ضرب کنید تا به مساحت مستطیل برسید. بطور کلی فرمول مساحت مستطیل:

- مساحت مستطیل = طول × عرض

محاسبه محیط مستطیل

برای بدست آوردن محیط مستطیل تنها چیزی که نیاز دارید، محاسبه طول و عرض های مستطیل است که باید یک طول را به اضافه یک عرض کنید و سپس جواب بدست آمده را ضربدر 2 نمائید. اما بطور کلی فرمول محیط مستطیل:

- محیط مستطیل = ( طول + عرض) × ۲

ویژگی‌های مستطیل

ضلع کوچک مستطیل را عرض مستطیل می‌نامیم و معمولاً با حرف اول معادل انگلیسی آن، یعنی ww نشان می‌دهیم. همچنین، ضلع بزرگ را طول می‌نامیم و معمولاً با ll نشان می‌دهیم.قطر مستطیل نیز، پاره‌خطی است که دو رأس مقابل را به هم متصل می‌کند. طول، عرض و قطر مستطیل در شکل زیر نشان داده شده‌‌اند.

 

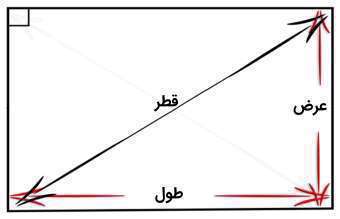
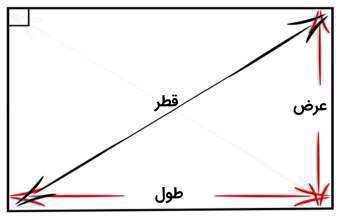
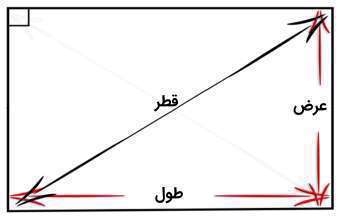
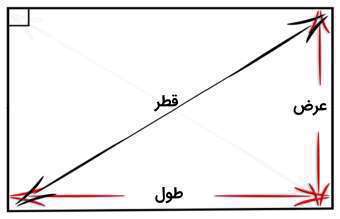
قطر مستطیل چیست؟

همان‌طور که گفتیم، قطر یک پاره‌خط است که دو رأس مقابل یک مستطیل را به هم وصل می‌کند. هر مستطیل دو قطر دارد که در شکل زیر نشان داده شده است.

دو قطر مستطیل هم‌اندازه هستند و یکدیگر را در مرکز قطع می‌کنند. زمانی که یک قطر مستطیل را رسم کنیم، مستطیل تبدیل به دو مثلث قائم‌الزاویه می‌شود که قطر مستطیل، وتر آن مثلث است. بنابر قضیه فیثاغورس می‌توان طول وتر مثلث یا همان قطر مستطیل را محاسبه کرد. اندازه قطر برابر است با مجذورِ مجموعِ مربعِ طول و مربعِ عرض:

(²عرض+²طول)√ = قطر

به عبارت دیگر، اگر اندازه طول ll، اندازه عرض ww و اندازه قطر dd باشد، با توجه به اینکه طول و عرض بر هم عمود هستند و همراه با قطر یک مثلث قائم‌الزاویه را تشکیل می‌دهند، می‌توان نوشت:

d2=w2+l2⇒d=√w2+l2d2=w2+l2⇒d=w2+l2

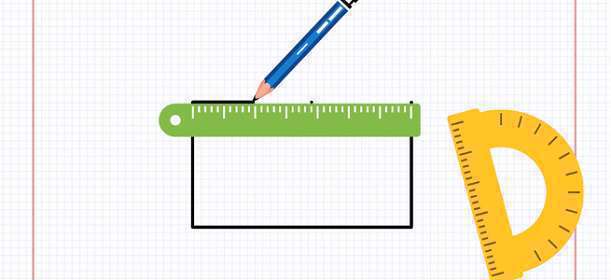
رسم مستطیل

برای رسم مستطیل‌ به نقاله، خط‌کش و مداد نیاز داریم. با استفاده از نقاله، می‌توان زاویه را اندازه گرفت. با کمک خط‌کش نیز می‌توان خطوط را رسم کرد و طول خطوط را اندازه گرفت. برای رسم مستطیل، پاره‌خطی به طول دلخواه مورد نظر رسم کنید. مثلاً ابتدا یک خط افقی را به عنوان طول مستطیل‌ رسم کنید. اکنون مرکز نقاله را روی دو انتهای پاره‌خط گذاشته و زاویه ۹۰ درجه را تعیین و با مدار مشخص کنید.

در مرحله بعد، خط‌کش را به‌گونه‌ای قرار دهید که نقطه ابتدایی آن، یکی از نقطا انتهایی پاره‌خط و نقطه دیگر آن، نقطه‌ای باشد که با زاویه ۹۰ درجه توسط نقاله مشخص کرده‌اید. پاره‌خطی به اندازه عرض مورد نظر رسم کنید. همین کار را برای دو نقطه دیگر در سمت دیگر پاره‌خط انجام دهید. اکنون سه ضلع داریم. ضلع دیگر را رسم کرده و شکل را تکمیل کنید.

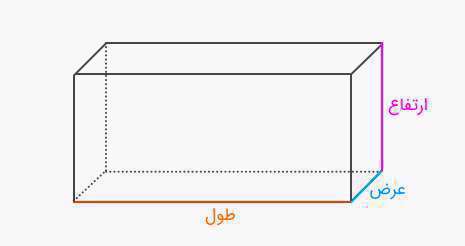
مساحت مکعب مستطیل چگونه به دست می آید؟

مکعب مستطیل یک شکل هندسی سه‌بعدی است که شش رویه یا وجه مستطیل شکل دارد. همه زوایای مکعب مستطیل قائمه هستند. مکعب مربع یا همان مکعب، حالت خاصی از مکعب مستطیل است.

مکعب مستطیل یکی از احجام هندسی است و ویژگی‌های آن:
- مکعب مستطیل دارای ۸ رأس، ۱۲ ضلع و ۶ وجه است.
- تمام وجه‌های روبه‌رو در مکعب مستطیل برابر هستند.
- مکعب مستطیل دارای مقاطع مستطیلی است.

فرمول مساحت مکعب مستطیل

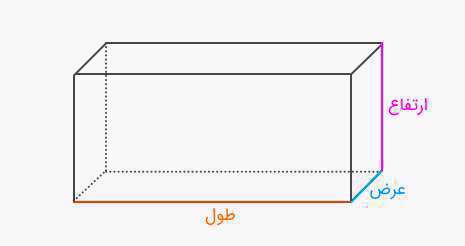
مکعب مستطیل شکل زیر را در نظر بگیرید که طول، عرض و ارتفاع آن مشخص شده است. از آنجا که وجه‌های روبه‌رو یکسان هستند، مساحت مکعب مستطیل را می‌توان به صورت زیر نوشت:[ (ارتفاع× طول) + (عرض × ارتفاع) + (عرض × طول) ] × ۲ = مساحت مکعب مستطیل

در واقع، اگر مکعب مستطیل را باز کنیم، شش مستطیل خواهیم داشت که دو به دو با هم برابر هستند و مساحت سطح مکعب مستطیل، برابر با مجموع مساحت این مستطیل‌ها است. 

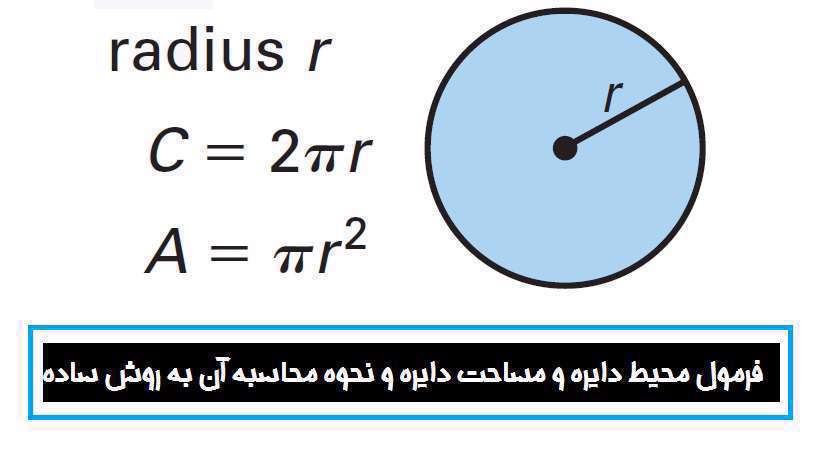
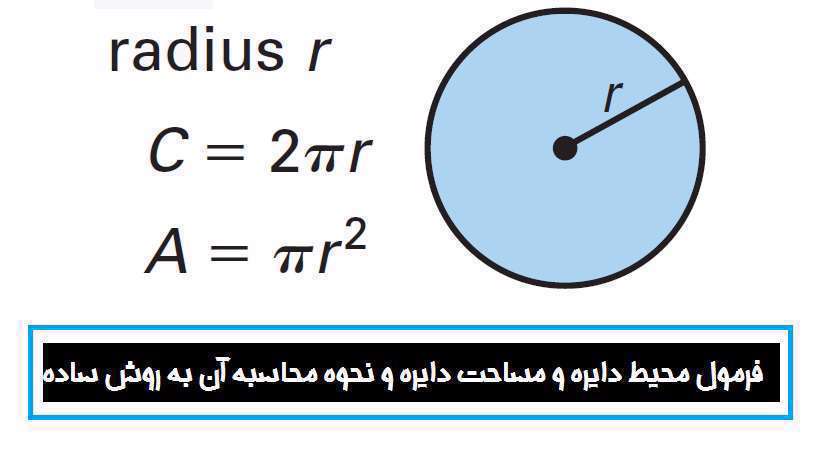
مساحت دایره

مساحت دایره برابر است با حاصلضرب مربع شعاع دایره در عدد پی. در هندسه، مساحت دایره (یا به عبارت دقیق‌تر مساحت قرص دایره) برابر است با حاصلضرب مساحت مربعی که ضلعش برابر شعاع دایره است در نسبت محیط دایره به قطر آن (که همیشه عدد ثابت است و با حرف {\displaystyle \pi }  نشان داده می‌شود). یعنی:

{\displaystyle \pi r^{2}}  = {\displaystyle (r\times r)\times ({\frac {C}{d}})}  = مساحت

مساحت متوازی الاضلاع 

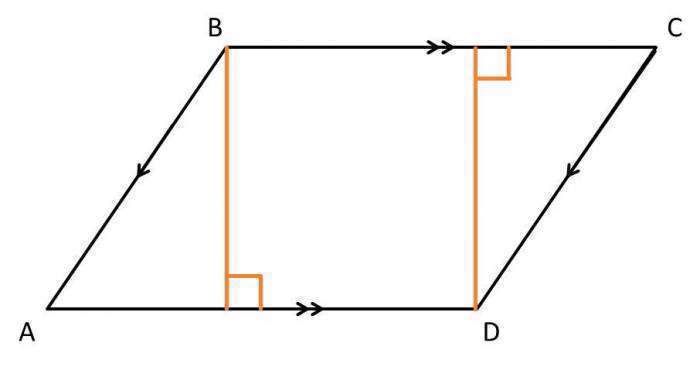
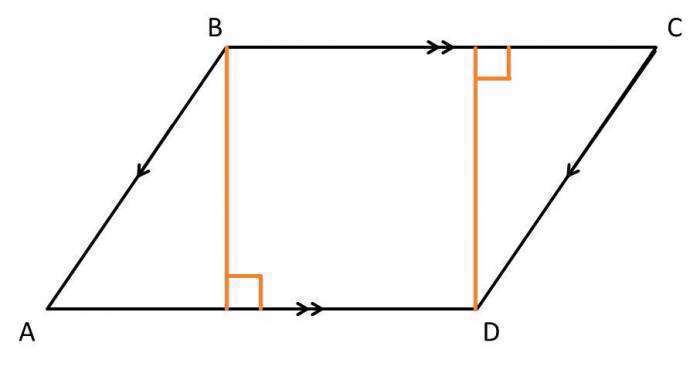
متوازی‌الاضلاع یک شکل هندسی با چهار ضلع است و همان‌گونه که از نامش بر می‌آید، اضلاع مقابل آن، دو به دو موازی هستند. یک خاصیت دیگر متوازی‌الاضلاع این است که زاویه‌های مجاور آن مکمل هستند، یعنی مجموع اندازه آن‌ها برابر با ۱۸۰ درجه است.

فرمول مساحت متوازی الاضلاع چیست؟

برای بدست آوردن مساحت متوازی الاضلاع تنها به 2 چیز نیاز دارید که کار آسانی می باشد. اولین اندازه مورد نیاز برای شما، ارتفاع متوازی الاضلاع است و دومین عدد مورد نیاز، قاعده است که همان ضلع AD است.

بعد از محاسبه این دو عدد که حال بستگی به مسئله دارد که آیا این اعداد را مشخص کرده باشد یا خیر! اگر مشخص شده باشد کار شما آسان می باشد و اگر مشخص نکرده باشد باید بر اساس داده های مسئله اقدام به حل کنید. اینک باید دو عدد مشخص شده را با یکدیگر ضرب کنید که بطور کلی فرمول مساحت متوازی الاضلاع با توجه به تصویر بالا مطابق زیر خواهد بود؛

AD × h

با توجه به اینکه چه اطلاعاتی درباره متوازی‌الاضلاع در اختیار داشته باشیم (مانند طول اضلاع، طول قطرها، ارتفاع و زاویه بین اضلاع)، با فرمول‌های مختلفی می‌توانیم مساحت متوازی الاضلاع را محاسبه کنیم. در ادامه، فرمول‌های مختلف محاسبه مساحت متوازی الاضلاع را برای حالت‌های گوناگون ارائه می‌کنیم.

مساحت متوازی الاضلاع با قاعده و ارتفاع

وقتی اندازه یک ضلع و ارتفاع متناظر با آن را داشته باشیم، برای به دست آوردن مساحت، کافی است ارتفاع را در آن ضلع (قاعده) ضرب کنیم.

A=a⋅hA=a⋅h

مساحت متوازی الاضلاع با دو ضلع و زاویه بین آن‌ها

در برخی موارد، اندازه دو ضلع متوازی‌الاضلاع و زاویه بین آن‌ها را داریم. در چنین مواقعی، مساحت متوازی الاضلاع برابر با حاصلضرب دو ضلع در سینوس زاویه بین آن‌ها است.

A=a⋅bsin(α)A=a⋅bsin⁡(α)

مساحت متوازی الاضلاع با دو قطر و زاویه بین آن‌ها

اما اگر اندازه دو قطر و زاویه بین آن‌ها را داشته باشیم، چگونه می‌توانیم مساحت را به دست آوریم؟ در این حالت، مساحت متوازی الاضاع برابر با نصف حاصلضرب دو قطر در سینوس زاویه بین آن‌ها است.

A=12d1⋅d2⋅sin(α)A=12d1⋅d2⋅sin⁡(α)

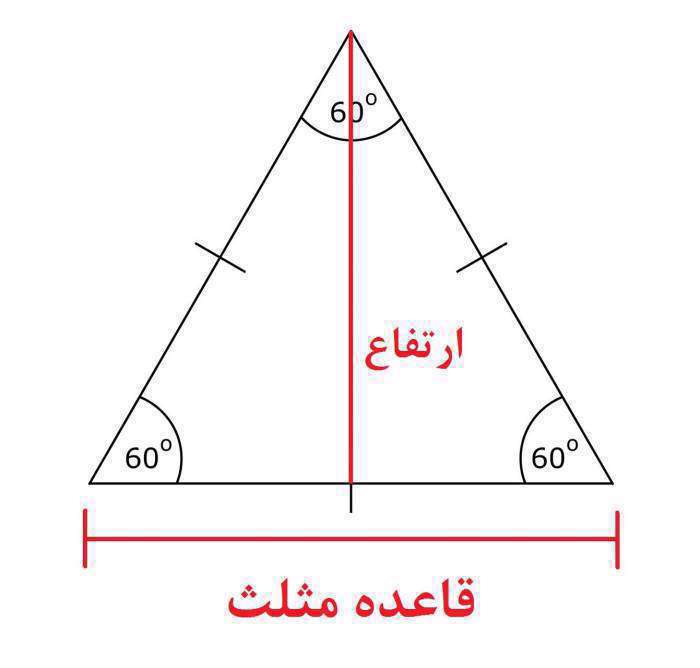
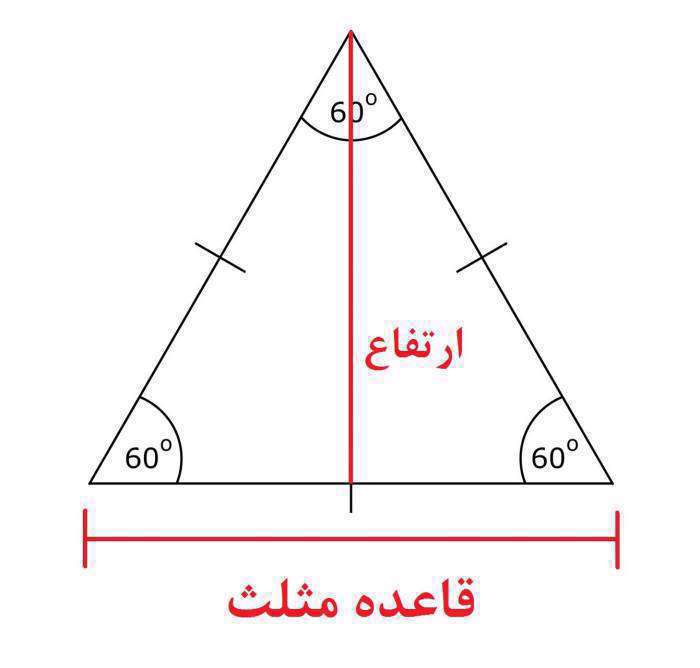
فرمول محاسبه مساحت مثلث

مثلث از اشکال هندسی پایه و پرکاربرد در مسائل هندسه و ریاضی می باشد که شاید برای محاسبه مسائل ترکیبی نیاز به محاسبه محیط و مساحت مثلث داشته باشید که دو فرمول ساده هستند.در  مثلث یک ضلع، قاعده و خطی از وسط می گذرد، که به نام ارتفاع مثلث می گویند. از این رو اگر شما قصد محاسبه مساحت مثلث را دارید، باید قاعده را ضربدر ارتفاع کنید و در نهایت جواب بدست آمده را تقسیم بر 2 کنید. در کل فرمول مساحت مثلث طبق زیر می باشد؛

(قاعده مثلث × ارتفاع) ÷2

---