تمرین اینترنتی طبقه بندی مثلث ها

اهداف

دانش آموز باید:

وسایل لازم

طرح درس

مبنای این درس، مسئله ای هندسی است که شرایطی را برای دانش آموزان فراهم می کند تا با مطالب بسیاری درباره ی مثلث ها و فضای مرتبط با آن ها آشنا شوند.

مفاهیم ارائه شده در این درس را می توان به عنوان آخرین درس در مورد مثلث ها دانست. در ا ین درس، خلاصه ی همه ی مطالبی که دانش آموزان می بایست یاد بگیرند، وجود دارد. از مسائل طرح شده در این درس نیز می توان به عنوان امتحان پایان دوره ی درس مثلث ها استفاده کرد.

مسئله ی طبقه بندی مثلث ها:

پاره خط AB در صفحه رسم شده است. تمام نقاط C را در صفحه پیدا کنید که مثلث ABC یکی از انواع زیر بشود:

- قائم الزاویه

- متساوی الساقین

- حاده الزاویه

- مختلف الاضلاع

- منفرجه الزاویه

- متساوی الاضلاع

قبل از آموزش این درس، شما باید خودتان این مسئله را تمرین کرده باشید. یک کپی از فعالیت مثلث ها را تهیه کنید. حالا صفحه را طبق این که مثلث را بر اساس زاویه ها یا اضلاع طبقه بندی می کنید، به چند بخش تقسیم کنید. راه حل مسئله را می توانید در قسمت تمرین اینترنتی ببینید. سعی کنید مسئله را بدون مراجعه به جواب، حل کنید. در این صورت می توانید سؤالات بهتری را در حین تدریس به   دانش آموزان طرح کنید.

 

برگه فعالیت مثلث ها

در ضمن، یک کپی از صفحه ی کار در کلاس را به صورت برگ شفاف (transparent) جهت ارائه به دانش آموزان در هنگام تدریس، آماده داشته باشید.

برای شروع، سؤالات زیر را از دانش آموزان بپرسید:

بعد از مقدمه چینی، صفحه ی کار کلاسی را روی دستگاه اورهد قرار دهید. توضیحات آن را برای دانش آموزان بخوانید. سپس از آنان بخواهید نقطه ای به نام C را نشان دهند که یک مثلث قائم الزاویه پدید آید. داوطلبی را انتخاب کنید تا پای اورهد بیاید و بدون هیچ توضیحی فقط یک نقطه (C) روی برگ شفاف (transparent) مشخص کند. سپس، با دانش آموزان بحث و گفتگو کنید. آیا این نقطه، مثلث قائم الزاویه درست می کند؟ چگونه فهمیدید؟ در خلال بحث، سؤالاتی را مطرح کنید تا دانش آموزان را به تفکر بیشتر و سریع تر وادارید، اما مراقب باشید که نظرات خود را مطرح نکنید.

پس از بحثی کوتاه، برگه های کار کلاسی را بین دانش آموزان پخش کنید و به سؤالات دانش آموزان در مورد این برگه جواب دهید. وقتی سؤالات آن ها تمام شد و آماده ی پاسخ دادن شدند، یک یا دو دقیقه به آن ها فرصت دهید که هر کدام به تنهایی در مورد مسئله فکر کنند و انواع مختلف را تعیین کنند. (بیش تر از یکی دو دقیقه وقت لازم نیست. هنگامی که شما درباره ی مثلث قائم الزاویه بحث می کنید، اغلب دانش آموزان درباره ی نقاطی که انواع دیگر مثلث را پدید می آورند، فکر خواهند کرد.)

پس از آن، 5 دقیقه فرصت دهید تا دانش آموزان، یافته های خود را با همکلاسی خود در میان بگذارند. در این صحبت ها، دانش آموزان اغلب اشکالات خود را متوجه می شوند. همچنین، وقتی دو دانش آموز با هم کار می کنند، اکثر نقاط و یا حتی تمام نقاط مربوط به مثلثی خاص را پیدا می کنند.

بقیه ی وقت کلاس را به بحث در مورد یافته های دانش آموزان اختصاص دهید. افراد مختلف را برای تعیین 6 نوع مثلث مورد نظر انتخاب کنید. در خلال بحث، قضایای مورد نیاز برای یافتن جواب این مسئله را مرور کنید. به عنوان مثال، دایره ای به مرکز وسط AB ، نقاطی را مشخص می کند که مثلث ABC ، قائم الزاویه و AB وتر آن خواهد بود. علت این مسئله، قضیه ی زیر است:

"زاویه ی محاطی یک نیم دایره، قائمه است."

پرسش هایی برای دانش آموزان

- مکان هندسی نقاطی که مثلث متساوی الساقین پدید می آورند، سه دایره است. آیا این دایره ها یکسانند یا متفاوت؟

(دایره ای به قطر AB مثلث های متساوی الساقین را مشخص می کند که AB وتر آن است. دو دایره ی دیگر، مثلث هایی را شامل می شوند که AB یکی از ساق های مساوی مثلث است.)

- دو خط عمود بر AB در نقاط A و B رسم کنید. این خطوط، نقاطی را نشان می دهند که مثلث های قائم الزاویه پدید می آورند. دو دایره به مراکز A و B مکان هندسی نقاطی هستند که مثلث متساوی الساقین می سازند. نقاط مشترک بین این دو مکان هندسی، چه مثلث هایی را نشان می دهند؟

(نقاطی هستند که مثلث هایی با زوایای 45، 45 و 90 درجه پدید می آورند.)

- نقاط تقاطع دو دایره به مراکز A و B و شعاع AB با خط عمود منصف AB، مشخص کننده ی چیست؟

(این دو نقطه، مشخص کننده ی دو مثلث متساوی الاضلاع هستند که پاره خط AB قاعده ی آن است. )

پس از امتحان

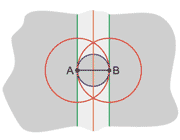
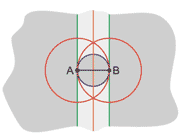
1- برگه هایی را که بین دانش آموزان توزیع کرده بودید، جمع آوری کنید تا به میزان درک هر دانش آموز در مورد این مسئله پی ببرید. جواب کامل مسئله شکل زیر خواهد بود:

در نمودار فوق، خطوط سبز و دایره ی آبی، مکان هندسی نقاطی هستند که مثلث قائم الزاویه پدید می آورند. خط نارنجی و دایره ی قرمز مشخص کننده ی مثلث های متساوی الساقین است. مناطق خاکستری تیره، مثلث هایی با اضلاع مختلف و زاویه ی منفرجه پدید می آورند. قسمت خاکستری روشن، مثلث هایی با اضلاع مختلف و زاویه ی حاده درست می کنند.

2- فرصت دهید تا دانش آموزان با استفاده از بخش اینترنتی، کار خود را ارزیابی کنند.

توسعه

از دانش آموزان بخواهید به مسئله ی زیر توجه کنند. احتمال این که یک نقطه ی انتخاب شده ی تصادفی در صفحه، مثلث با زوایای حاده درست کند، چقدر است؟ [صفر. ممکن است به نظر دانش آموزان این امکان صفر باشد، چون تعداد معدودی از نقاط صفحه، مثلث حاده الزاویه می سازند. ممکن است آن ها چنین راه حلی را در ذهن خود مجسم کنند: اگر در نقاط A و B خطوطی عمود بر AB رسم شود، فقط نقاطی که روی این خطوط قرار دارند می توانند مثلث حاده الزاویه درست کنند. به عبارت دیگر اگر این نقطه خارج از دو خط عمود انتخاب شود، مثلث منفرجه الزاویه به دست می آید. طول بین دو نقطه A و B، پاره خط AB است که محدود است. در حالی که طول بین نقاط خارج از AB، نامحدود است. بنابراین احتمال با 0? محدود/نامحدود برابر است.

بررسی اجرای طرح درس در کلاس

مترجم: مهدی صباغی

تنظیم: نسرین صادقی