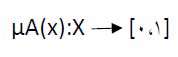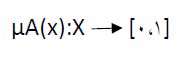سیزدهمین دوره از پروژه های دانش آموزی تبیان نیز با یاری خداوند و حضور پر شور شما دوستان و علاقمندان به پایان رسید.
در این دوره از جشنواره از 20 استان کشور در سه بخش به تفکیک، 350 گروه در بخش غرفه های نمایشگاهی، 650 گروه در بخش سمینارهای علمی و 750 گروه در بخش مسابقات دانش آموزی از مدارس و پژوهش سراهای دانش آموزی سراسر کشور انتخاب شده اند و به جشنواره کشوری دعوت شده اند.
که تعداد 53 گروه در بخش سمینارهای علمی مقام برتر را کسب نمودند.
بر آن شدیم تا با معرفی پروژه های گروه های برتر علاوه بر قدردانی از این دوستان نوآور، زمینه ای را برای ایده پروری سایر پژوهشگران علاقمند فراهم آوریم.

مقطع: دوره دوم متوسطه
موضوع: منطق و سیستم های فازی
نام مدرسه: پژوهشسرای دکتراذکایی ناحیه یک همدان
نام استاد: آقای حسن ختن لو
دانش آموزان: زهرا ختن لو، مینا یعقوبی منصور، فاطمه نایینیان
چکیده:
براي حل مسائل روز نيازمند يك سيستم تصميم گيرنده هستيم. سيستمي كه با تصميم هاي هوشمندانه خود به كمك انسان ها بيايد. در علم رياضيات راه حل هاي متفاوتي براي تصميم گيري وجود دارد ؛ از قبيل سيستم هاي خبره، درخت تصميم گيري و ... كه ما در مطالعات خود به اين نتيجه رسيديم كه منطق فازي راه حل مناسبي براي اين قبيل مسائل است. بنابراين درصدد برآمديم كه مطالعات خود را در زمينه منطق فازي گسترش دهيم.

با مراجعه به كتب مربوطه به گسترش دامنه اطلاعات خود پرداختيم، علاوه بر اين از مقاله ها و مطالب موجود در اينترنت نيز استفاه كرديم . همچنين توانستيم با مصاحبه با اساتيد دانشگاه اين دانش را در ذهن خود بنيادين كنيم.

خلاصه اي از اين اطلاعات بدين شرح است :
منطق فازي: در منطق صريح مقادير درستي به دست آمده داراي دو مقدار هستند؛ درست يا غلط. كه از لحاظ رياضي مي توان آنها را معادل ( ١ و ٠)  در نظر گرفت، ولي در منطق فازي، مقادير درستي چند مقداري بوده؛ مانند : كاملاً درست، تا حدي درست، كاملا غلط، خيلي درست، كه از لحاظ عددي بين ٠ و ١ هستند .

مجموعه فازي: در تئوري مجموعه هاي صريح، يك جزء يا به يك مجموعه تعلق دارد يا ندارد. اما در تئوري مجموعه هاي فازي، درجه هاي مختلف عضويت بين ( ١و ٠)  قابل حصول است . بنابراين تابع عضويت μA(x) به يك مجموعه فازي مانند A نسبت داده مي شود كه اين تابع هر عضو در مجموعه مرجع  X را به بازه [ ١ و ٠ ] مي نگارد . اين نگاشت به صورت زير است :
براي حل مسائل و تصميم گيري فازي از سيستم هاي فازي استفاده مي شود كه سيستم هاي فازي از قواعد مجموعه هاي فازي و منطق فازي استفاده مي كند.

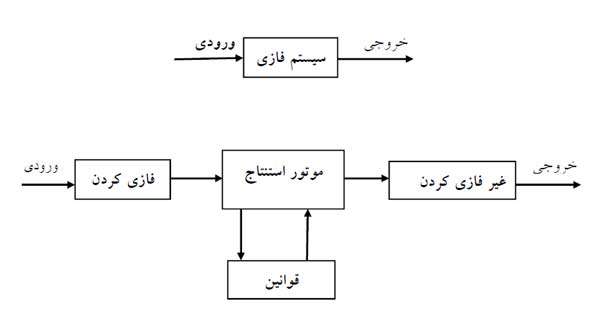
يك سيستم فازي شامل ٤ قسمت مي باشد :
١. فازي كردن
٢. موتور استنتاج 
٣. قوانين فازي خروجي ورودي
٤. غير فازي كردن

با توجه به اطلاعات به دست آمده، در پي طراحي و بيان مسئله هستيم كه آن را با سيستم هاي فازي حل كنيم و سپس آن را در نرم افزار متلب پياده سازي خواهيم كرد.

بخش پژوهش های دانش آموزی تبیان، تهیه و تنظیم: نسرین صادقی