دنباله اعداد فیبوناچی
فکر می کنید به چند طریق می‌توانید از یک پلکان که دارای n پله است، بالا بروید، در صورتی که در هر گام فقط بتوانید یک یا دو پله را طی کنید؟ برای یافتن پاسخ این مسأله، ابتدا یک حالت ساده را در نظر می‌گیریم. فرض کنید که پلکان چهار پله دارد. شما می‌توانید با چهار گام کوچک ( یک پله ای ) مسیر را طی کنید و یا این که دو گام بزرگ ( دو پله ای ) یا یک گام بلند و دو گام کوچک بردارید. کلیه ی حالت های ممکن در شکل زیر نمایش داده شده است. پله هایی که با علامت مشخص شده اند، پله هایی هستند که روی آن قدم گذاشته اید.
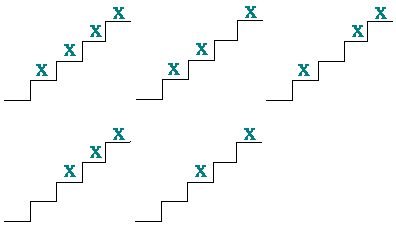
در واقع این مسأله را با یک استراتژی بسیار ساده می‌توان حل کرد. کافی است مسأله را کمی کوچک یاساده کنیم. آخرین گام یک گام کوچک یا یک گام بزرگ است. در واقع تعداد راه هایی که می‌توان پلکان را طوری طی کرد که به پله ماقبل آخر رسید، حل مسأله برای یک پله کم تر ( n-1 پله ) است و تعداد راه هایی که می‌توان از آن به دو پله پایین تر رسید، حل مسأله برای دو پله کم تر ( n-2 پله ) خواهد بود. در مثال بالا سه مسیر مختلف وجود دارد که به پله ی سوم می‌رسد و دو مسیر وجود دارد که به پله ی دوم منتهی می‌شود. حال باید مسأله را برای این دو حالت کوچک تر حل کنیم. ما دوباره هر یک از این دو حالت را به حالات کوچک تر مشابه تقسیم می‌کنیم. این روش را "حل بازگشتی " می‌نامند. در واقع ما هر بار مسأله را به مسأله ای شبیه خودش - اما کوچک تر از آن - تبدیل می‌کنیم. تعداد کل مسیرها برابر مجموع مسیرهایی که به پله ی ماقبل آخر رسیده و همین طور مسیرهایی که به دو پله قبل از پله ی آخر منتهی شده اند، می‌باشد. می‌توانید بگویید چرا؟
اگر همین طور مسأله را به مسأله های کوچک تر تقسیم کنیم، در پایان به جایی می‌رسیم که حل آن برای ما بسیار ساده است: به چند طریق می‌توان دو پله را طی کرد؟ و پس از حل آن، دوباره مسیری را که برای حل مسأله طی کرده ایم، باز می‌گردیم.
| این مسأله را می‌توان با دنباله ی اعداد فیبوناچی نیز حل کرد. دنباله ی فیبوناچی یک دنباله ی بازگشتی است که در آن اعداد اول و دوم برابر یک می‌باشند. هر عدد این دنباله از جمع کردن دو عدد قبلی به دست می‌آید. چند عدد ابتدایی این دنباله عبارتند از:.... و 13و 8 و 5 و 3 و 2 و 1 و 1، چون: ...و13=5+8 و 8=3+5 و 5=2+3 و 3=1+2 و 2=1+1 اگر عدد n ام این دنباله را با fn نشان دهیم، آن گاه می‌توان دنباله را با فرمول بازگشتی زیر مشخص نمود: fn=fn-1+fn-2 , f1=1 , f2=1 اگر دقت کنید متوجه می‌شوید که f1 دقیقاً برابر تعداد راه های ممکن برای بالا رفتن از یک پله، f2 برابر راه های ممکن برای دو پله و به همین ترتیب fn تعداد مسیرهای ممکن برای رسیدن به بالای یک پلکان n تایی است.
مسائل بسیاری را می‌توان با استفاده از دنباله ی اعداد فیبوناچی حل نمود. این دنباله در سال 1202 میلادی توسط یک ایتالیایی به نام " لئوناردو فیبوناچی " (Leonardo Fibonacci) ابداع شد. در واقع او در جستجوی راه حل یک مسأله بود. مسأله به این صورت است که : " اگر هر جفت خرگوش در هر ماه یک جفت خرگوش جدید به دنیا بیاورند و خرگوش های جدید نیز پس از گذشت یک ماه، به دوران باروری برسند ( با فرض این که هیچ خرگوشی نمیرد )، تعداد خرگوش ها را در ماه n ام به دست آورید. "  | ||
بعدها، یوهان کپلر (Johannes Kepler) خاصیت جالب دیگری از این دنباله را کشف کرد. او نسبت دو جمله ی متوالی این دنباله را محاسبه نمود و متوجه شد که این نسبت به عدد
اعداد فیبوناچی را در بسیاری از موارد طبیعی نیز می‌توانید مشاهده کنید. آرایش برگ‌ها و گل های بسیاری از گیاهان به صورت دو پیچه (spiral) است. معمولاً تعداد پیچه های ساعت گرد با تعداد پیچه های پادساعت گرد تفاوت دارد. این دو عدد در اغلب مواقع دو عدد متوالی از رشته ی فیبوناچی هستند. به شکل زیر توجه کنید:   | ||
| این الگو را می‌توان در گل برگ‌ها یا دانه های بسیاری از گیاهان مثلاً آناناس، گل داوودی، گل کلم، میوه های کاج و ... مشاهده کرد. شاید دلیل آن این باشد که وقتی دانه‌ها ( یا گل برگ‌ها ) به این صورت قرار گیرند، بدون توجه به اندازه ی آن ها به طور یکنواخت و فشرده در کنار هم جای می‌گیرند؛ یعنی با این که عده ای از دانه‌ها کوچک تر از بقیه هستند، در هیچ ناحیه ای تراکم تغییر نمی کند و فضای خالی دیده نمی شود. با استفاده از applet زیر می‌توانید پیچه های متعدد را مشاهده کنید.  | ||
این دنباله خواص جالب دیگری نیز دارد، مثلاً: f2n+f2n+1=f2n+1 f2n-fn+1fn-1=(-1)n-1 f2n-fn+2fn-2=(-1)n f2n-fn+3fn-3=4(-1)n-1 با توجه به سه فرمول آخر، آیا می‌توانید فرمولی برای محاسبه f2n-fn+k .fn-k | ||
| ارائه کنید؟ می‌توانید فرمول خود را اثبات کنید؟ اگر تمایل دارید تا درباره ی اعداد فیبوناچی مطالب بیش تر ی بدانید، می‌توانید به سایت زیر مراجعه کنید: | ||
http://www.mcs.surrey.ac.uk/Personal/R.Knott/fibonacci/fibnat.html | ||
آیا می‌توانید توضیح دهید که چرا تساوی بالا برقرار است؟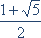
نزدیک می‌شود. این نسبت، عددی شناخته شده بود که " عدد طلایی " نامیده می‌شد.
