دانستی های ریاضیات
در این مقاله فرمول های مورد نیاز برای محاسبه اندازه زاویه ها و تعداد پاره خط ها را ارائه می دهیم.
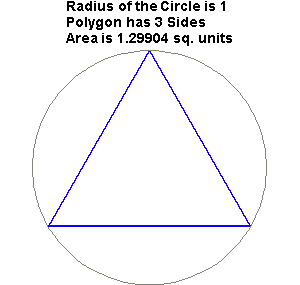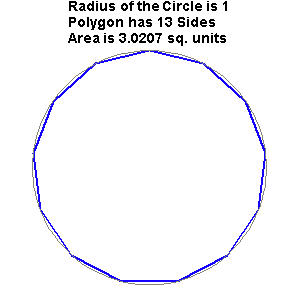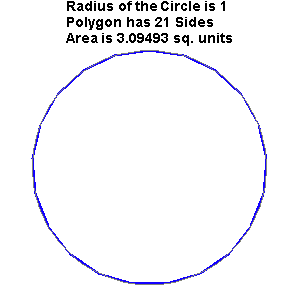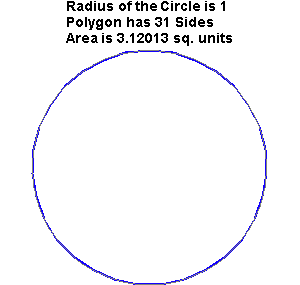
۱-برای پیدا كردن مجموع زوایای داخلی یك n ضلعی از روش زیر استفاده می كنیم:
(n-2)× 180
مثال۱:مجموع زاویه های داخلی یک هشت ضلعی منتظم چند درجه است؟
مثال۲:اگرمجموع زاویه های داخلی یک nضلعی ۱۴۴۰ درجه باشد تعداد ضلع های این nضلعی چندتاست؟
۱۴۴۰÷۱۸۰=۸
۸+۲=۱۰
۱۰ضلعی
۲-مجموع زاویه های خارجی هر nضلعی محدب برابربا ۳۶۰ درجه می باشد.
نکته:زاویه خارجی زاویه ای است که از امتدادیک ضلع باضلع دیگر ایجاد می شود.
۳-اندازه هر زاویه داخلی یک n ضلعی منتظم از دستور زیر به دست می آید:
(n-2)×180÷n
مثال1:اندازه هر زاویه داخلی یک ۹ضلعی منتظم چند درجه است؟
(۹-۲)×۱۸۰ ÷۹=۱۴۰
نکته:هردو زاویه داخلی و خارجی مجاور به هم با هم مکملند.
مثال2:اگر اندازه هر زاویه داخلی یک n ضلعی منتظم ۱۵۶درجه باشد تعداد ضلع های این nضلعی منتظم چندتاست؟
۱۸۰ - ۱۵۶=۲۴
اندازه هر زاویه خارجی= ۲۴درجه
۳۶۰ ÷ ۲۴=۱۵
۱۵ضلعی منتظم
مثال3:در کدام چند ضلعی مجموع زاویه های داخلی ۴برابر مجموع زاویه های خارجی است؟
(n-۲)×۱۸۰=۴×۳۶۰=۱۴۴۰
۱۴۴۰÷۱۸۰=۸
۸+۲=۱۰
۱۰ضلعی
مثال۳:اگراندازه هر زاویه خارجی یک nضلعی منتظم ۳۶ درجه باشد تعدادضلع های این nضلعی منتظم چند تاست؟
۳۶۰ ÷ ۳۶=۱۰
۴-برای پیدا كردن تعداد زاویه های شکلی که ازچند زاویه با رأس مشترک تشکیل می شود از دستور زیر استفاده می كنیم:
2÷(تعداد خط×تعداد فاصله)
۵- هرگاه چند نقطه متمایز ( جدا از هم ) برروی یک خط راست باشند تعداد پاره خط ها را از فرمول زیر به دست می آوریم.
2 ÷ ( تعداد فاصله ها × تعداد نقطه ها ) = تعداد پاره خط ها
مثال : بر روی خطی هفت نقطه ی متمایز وجود دارد تعداد پاره خط ها را به دست آورید ؟
جواب : 21 = 2 ÷ ( 6 × 7 ) = تعداد پاره خط ها
مثال۲:اگر بر روی خط راستی ۲۱ پاره خط وجود داشته باشد , چند نقطه روی این خط وجود دارد؟
۲۱×۲=۴۲
۴۲=n(n-۱)
۴۲=۷(۷-۱)
۷نقطه
6-تعداد قطرهای یك nضلعی محدب را به صورت زیر بدست می آوریم:
n(n-۳)÷۲
سوال:یک ۶ضلعی محدب چند قطر دارد؟
۶(۶-۳)÷۲=۶×۳÷۲=۹
۹قطر دارد
۷-برای جمع بستن اعداد متوالی از ۱ تا n از دستور زیر استفاده می كنیم:
n(n+۱)÷۲
مثال: اگر تمام اعدادطبیعی متوالی از 1 تا 20 را جمع كنیم ، حاصل جمع را حساب كنید.
جواب: 210=2÷ 20×(20+1)
۸-برای به دست آوردن تعداد اعداد متوالی(پشت سر هم) راه حل زیر مناسب است.
1+فاصله÷(عدد اول – عدد آخر)
مثال: از عدد 10 تا 20 چند عدد به كار رفته است؟
11=1+1÷(20-10) جواب
مثال:تعداد اعداد الگوی زیر چندتاست؟
۲ , ۵ , ۸ , ۱۱ , ... , ۸۹
(۸۹-۲)÷۳+۱=۳۰
۳۰عدد
البته می توان جمله nام را تشکیل داد سپس مقدارn را که همان تعداد جملات می باشد را تعیین کرد:
۳n -۱=۸۹
۳n=۸۹+۱=۹۰
n=۹۰÷۳=۳۰
۳۰عدد
9- برای به دست آوردن مجموع اعداد متوالی با فاصله های ثابت ابتدا تعداد اعداد را مشخص می کنیم سپس در میانگین دو عدد اولی و آخری ضرب می کنیم.
مثال:حاصل عبارت زیر را به دست آورید.
۵+۹+۱۳+۱۷+...+۸۱= ?
تعداد اعداد در این مجموع ۲۰تاست
۲۰×۴۳=۸۶۰
۸۶۰مجموع اعداد بالا
10- برای شماره گذاری صفحات كتاب از روش زیر استفاده می شود:
برای اعداد یك رقمی: 1-1×(1+صفحه)
برای اعداد دو رقمی: 11-2×(1+صفحه)
برای اعدد سه رقمی: 111-3×(1+صفحه)
مثال: كتابی 160 صفحه دارد. برای شماره گذاری این كتاب چند رقم به كار رفته است؟
جواب: 372=111-3×(1+160)
11-برای محاسبه ی زمان كار انجام شده دو نفر ، از فرمول زیر استفاده می كنیم:
مجموع كار÷ حاصل ضرب كار
مثال: علی كاری را 6 روز و حسین همان كار را در 4 روز انجام می دهد. اگر این دو باهم كار كنند، این كار را چند روزه انجام می دهند؟
جواب: 2/4 =(4+6)÷(4×6)
12-اگر ساعتی در هر شبانه روز چند دقیقه جلو یا عقب كار كند،برای محاسبه ی این كه پس از چه مدتی وقت درست را نشان می دهد ، از فرمول زیر استفاده می كنی
مقدارعقب مانده ,جلوافتاده÷۶۰×۱۲
مثال: ساعتی در هر شبانه روز 5 دقیقه جلو می افتد، این ساعت پس از چند شبانه روز وقت درست را نشان می دهد؟
جواب: 144=5÷60×12
13-برای محاسبه ی زاویه ی بین دو عقربه ی ساعت از این روش استفاده می كنیم:
زاویه ی بین دو عقربه=(ساعت×30)-(دقیقه×5/5)
مثال: ساعت 4:30 چه زاویه ای را نشان می دهد؟جواب:45=(4×30)-(30×5/5)
تهیه: مرکز یادگیری سایت تبیان