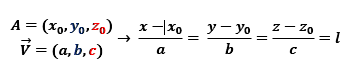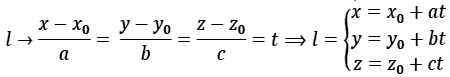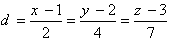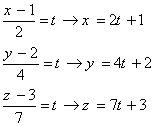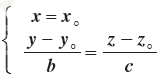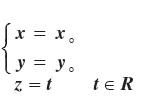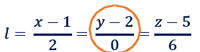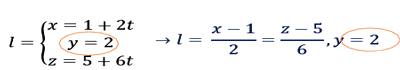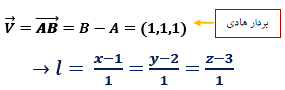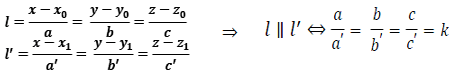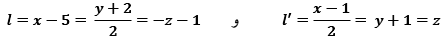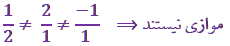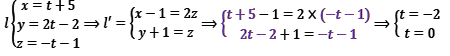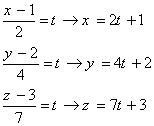معادله خط در فضای سه بعدی
معادله خط در فضای دو بعدی به صورت y=mx+b نشان داده می شود.در واقع در فضای دو بعدی برای نوشتن یه معادله خط به یک نقطه از خط و شیب آن خط احتیاج است.اما باید بدانیم بین خط در فضای سه بعدی با خط در فضای دو بعدی کاملاً تفاوت وجود دارد
معادله خط در فضای 3 بعدی زمانی مشخص می شود که:
1- یک نقطه روی خط را داشته باشیم.
3- برداری موازی با خط که با نام "بردار هادی" آن را می شناسیم، موجود باشد.بردار هادی را معمولا با حرف v یا u نسان می دهند.
اگر (x0,y0,z0) یک نقطه از خط باشد و ( 𝑉⃗ (a,b,c برداری موازی این خط یا همان بردار هادی خط.می توان به دو روش زیر معادله خط در فضا را بدست آورد،
معادله متقارن یا کانونیک
معادله پارامتریک
نوع دیگر نمایش معادله ی خط، نمایش پارامتریک معادله ی خط می باشدبرای نمایش پارامتریک معادله ی خط ابتدا معادله ی خط را برابر پارامتر 𝑡 قرار می دهیم و مولفه های 𝑥 ، 𝑦 و 𝑧 را
برحسب 𝑡 بدست میآوریم:
در معادلات فوق باید گفت که متغیرِ 𝑡 هر چیزی میتواند باشد. یعنی شما به 𝑡 هر مقداری بدهید مختصات نقطه ای
حاصل می شود که آن نقطه حتما روی خط خواهد بود.
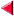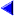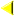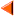 مثال: معادله متقارن و پارامتری خطی را بنویسید که از نقطه (1,2,3) گذشته و با خط v=(2,4,7) موازی باشد:
مثال: معادله متقارن و پارامتری خطی را بنویسید که از نقطه (1,2,3) گذشته و با خط v=(2,4,7) موازی باشد:
اکنون معادله پارامتری خط فوق را بدست می آوریم.
برای b=0 و c=0 به طریق مشابه می باشد.
2- اگرa=0 و b=0 در این صورت معادله متقارن خط به شکل زیر می باشد:
برای ادامه می توانیم از نکات فوق استفاده کنیم اما راهی هم که این نکته را حفظ نکنید .گر در معادله ی کانونیکِ خط، مخرجِ کسر برابر صفر شد، صورت را نیز مساوی صفر قرار می دهیم که عبارت 𝒚=𝟐 بدست می آید اما از کجا آمد؟ برای پاسخ به این سوال باید معادله ی پارامتریک این سوال رو هم بنویسیم. و در آخر به این نتیجه می رسیم چون مخرج کسر قسمت 𝒚 ، صفر شد، قسمت 𝒚 رو از پارامتریک قرض گرفتیم.
نکته:
وضعیت دو خط در فضا به صورت یکی از سه حالت زیر می باشد:
1- متوازی: دو خط همدیگرو قطع نمی کنند و دریک صفحه واقع هستند.
2- متقاطع: دریک نقطه همدیگرو قطع می کنند.
3- متنافر: همدیگرو قطع نمی کنند و در یک صفحه هم نیستند.
در شکل زیر به ترتیب از چپ به راست شماره های 1 تا 3 نشان داده شده اند.
 البته چون انطباق حالتی از توازی است بعد از چک کردن شرط موازی بودن دو خط اگر هر نقطه دلخواه از یک خط در خط دیگر هم صدق کند، آن دو خط منطبق بر هم هستند.
البته چون انطباق حالتی از توازی است بعد از چک کردن شرط موازی بودن دو خط اگر هر نقطه دلخواه از یک خط در خط دیگر هم صدق کند، آن دو خط منطبق بر هم هستند.
نکته: اگر دو خط موازی نبودند دو خط یا متقاطعند و یا متنافر. برای تشخیص متقاطع یا متنافر بودن باید معادله ی یک خط رو پارامتریک بنویسید،
𝑥 ، 𝑦 و 𝑧 اون خط رو بگذارید توی معادله ی اون یکی. دو تا معادله ازش استخراج می کنیم. از آن 𝑡 را حساب می کنیم. اگر 𝑡های حساب شده با هم برابر بود، دو خط متقاطعند اگر نبود. دو خط متنافر هستند.
مثال: وضعیت دو خط زیر را نسبت به هم چک کنید:
ابتدا باید موازی بودن را چک کنیم.
بنابر این دو خط متنافرند.
تهیه:پروین نظری- مرکز یادگیری تبیان