دامنه و برد توابع به بیان ساده
دامنه و برد توابع به بیان ساده
دامنه ی تابع مجموعه ی مقادیری است كه اگر به جای x (یا همان متغیر مستقل) قرار دهیم برای y (یا همان متغیر وابسته)عددی حقیقی بـه دسـت مـی آیـد.

به بیان دیگر دامنه ی تابع، مجموعه ی مقادیری است كه متغیر مستقل (x) می تواند داشته باشد و آن را با Df نمایش می دهیم .برد تابع نیز مجموعه ی مقادیری است كه به ازای x های دامنه برای y به دست می آید. در تابع f برد را با نماد R f نشان می دهند .به بیان دیگر برد یك تابع، مجموعه مقادیری است كه یك متغیر وابسته می تواند داشته باشد.
نکته: اگر تابع به صورت زوج مرتب نمایش داده شود، مجموعه ی همه عضوهای اول را دامنه و مجموعه ی همه ی عضوهای دوم را برد تابع می گوییم. دقت شود ممکن است گاهی تابعی داشته باشیم که بی نهایت زوج مرتب داشته باشد در این صورت باید تعریف دیگری برای محاسبه دامنه تابع ارائه کنیم.
نکته: حوزه تعریف، همان دامنه تابع است یعنی همان x ها و حوزه مقادیر ،همان برد تابع یعنی y هاست

 مثال: دامنه و برد تابع زیر را بیابید.
مثال: دامنه و برد تابع زیر را بیابید.
f ={(1 ,5 ),(0 ,0 ),( -1, 0),(2 , 1)} (1
پاسخ: {1,0,2,1-}=Df و {5,0,1}= Rf
2)  پاسخ: {1,2,3,4}=Df و Rf={B,C,D}
پاسخ: {1,2,3,4}=Df و Rf={B,C,D}
3) برد تابع f(x)=x2+3x با دامنه {0و1و3} کدام است؟
پاسخ: با جایگذاری نقاط دامنه در تابع، مقادیر برد محاسبه می شود.بنابر این Rf={0,4,18}


تعیین دامنه از روی نمودار تابع
برای تعیین دامنه و برد از روی نمودار باید دانش آموزان با مفهوم بازه ها آشنا باشند. برای تعیین دامنه تصور کنید که با دو دست خود از بالا و پایین نمودار را فشار داده و روی محور x ها بخوابانید اکنون می بینیم کدام نواحی روی محور X ها تصویر شده، همان را توسط بازه نشان می دهیم و به عنوان دامنه تابع در نظر می گیریم. و برای تعیین برد با دو دست از سمت راست و چپ فشار داده و روی محور y ها می خوابانیم و برد را تعیین می کنیم.در شکل زیر دامنه و برد را تعیین کرده ایم:
پاسخ: Df=[-1,+∞) و Rf =[1,+∞)


تعیین دامنه تابع از روی ضابطه آن
قبلا گفتیم گاهی ممکن است تابعی داشته باشیم که بی نهایت زوج مرتب داشته باشد در این صورت باید تعریف دیگری برای محاسبه دامنه تابع ارائه کنیم.تعیین دامنه به این معنی است که تابع در کدام نواحی (x ها) تعریف شده است و بدانیم تابع در چه نواحی تعریف نشده است، تا آنها را حذف کنیم. در حالت کلی در دو مورد زیر تابع تعریف نشده است.
1 ) تابع گویا در x هایی که مخرج را صفر کند تعریف نمی شود .
2 ) تابع رادیکالی در x هایی که زیر رادیکال را منفی کند تعریف نمی شود.
نکته: دامنه همه توابع به شکل چند جمله ای برابر R است.مثل توابع y=-2x3+5x و y=1/5 x2 - 1 .
بنابر این در توابع کسری به شکل گویا برای تعیین دامنه باید ریشه های مخرج را محاسبه کنیم و آنها را از دامنه حذف کنیم یعنی به این صورت
 {ریشه های مخرج} - Df=R
{ریشه های مخرج} - Df=Rو در حالت دوم برای تعیین دامنه توابع رادیکالی باید عبارت زیر رادیکال را بزرگتر مساوی صفر قرار دهیم .که در این حالت نامعادله تشکیل می شود .اگر نامعادله درجه 1 باشد به راحتی قابل حل است اما اگر نامعادله درجه 2 یا کسری باشد باید توسط جدول تعیین علامت حل شود.
نکته: عبارت زیر رادیکال با فرجه فرد می تواند مثبت یا منفی یا صفر باشد یعنی هیچ محدودیتی موجود نیست.
مثال: دامنه توابع زیر را بدست آورید.

مباحث تکمیلی
1)1) برای تعیین دامنه اگر به رادیکال با فرجه فرد برخوردید رادیکال را حذف کنید (فقط رادیکال نه عبارت زیر آن) و دامنه عبارت باقی مانده را بیابید. مانند :
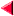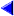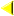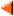

2) اگر عبارت رادیکالی با فرجه زوج به تنهایی در مخرج باشد باید برای تعیین علامت عبارت زیر رادیکال را بزرگتر از صفر قرار داد.(نه بزرگتر مساوی صفر، زیرا مخرج نمی تواند صفر باشد) مانند 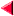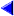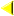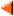

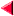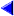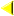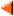
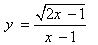
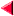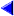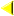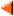

اکنون دامنه همه توابع فوق را محاسبه می کنیم.
1)
2)
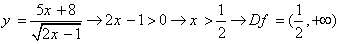
3)

4)

 برای تمرین بیشتر می توانید دامنه توابع زیر را بیابید:
برای تمرین بیشتر می توانید دامنه توابع زیر را بیابید:

تهیه: پروین نظری- مرکز یادگیری سایت تبیان


















