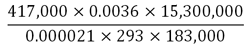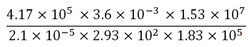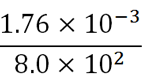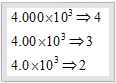اندازه گیری
مقدار یک کمیت از دو بخش تشکیل شده است، عدد و واحد مربوط به آن عدد.
تا کنون درباره واحد صحبت کردیم حال نگاهی به عدد می اندازیم.
بعضی از اعداد صحیح هستند و از شمارش به دست می آیند. برای مثال می گوییم 14 شاگرد در ردیف اول کلاس هستند یا این که یک دوجین تخم مرغ 12 عدد تخم مرغ دارد یا یک دقیقه 60 ثانیه است. بعضی از اعداد صحیح هستند اما نه آن گونه که می خواهیم. برای مثال عدد پی یا کسر 2/3 را با هر چند رقم که بعد از اعشار دارد، می نویسیم.
اما بسیاری از اندازه های کمیت های فیزیکی عدد صحیح نیستند. در تعیین فرایند تعداد واحدهای مساوی با آن کمیت اندازه گیری شده، خطایی وجود دارد. در این صورت باید نتیجه اندازه گیری را که یک عدد است به گونه ای بنویسیم که میزان خطا را نشان دهد. دو نوع خطا وجود دارد.
- صحت اندازه گیری: یعنی مقداری که از اندازه گیری به دست آمده است، چقدر به مقدار واقعی نزدیک است. معمولا پاسخ را نمی دانیم چون اگر مقدار واقعی را می دانستیم آن را به کار می بردیم.
- دقت اندازه گیری: یعنی در یک مجموعه اندازه گیری هر یک از اندزه ها چقدر به میانگین این اعداد نزدیک است. هر قدر عددی به میانگین نزدیک تر باشد آن اندازه گیری دقیق تر است. دقت در یک اندازه گیری به آسانی محاسبه می شود. دقت بالا معمولا اما نه همیشه، صحت زیاد را نشان می دهد. خطاهای سیستماتیک منجر به دقت زیاد اما صحت کم می شود.
بنابراین وقتی نتیجه یک اندازه گیری را می نویسیم، اعداد را به گونه ای می نویسیم که نشان دهنده دقت آن اندازه گیری باشد.
ارقام با معنی
به تمام ارقام یک عدد شامل ارقام مطمئن و اولین رقم نامطمئن ارقام با معنی گفته می شود. آخرین رقم یک عدد را رقم نامطمئن می گویند. یعنی این رقم دارای عدم قطعیت است. به عبارتی به هر رقمی که با اندازه گیری حاصل شده باشد، رقم با معنی گفته می شود.
وقتی عدد حاصل از یک اندازه گیری را می نویسیم، در رقم آخر عدم قطعیتی وجود دارد. هر چه رقم های اعشاری سمت راست ممیز بیشتر باشد اندازه گیری دقیق تر می باشد. به طور تقریب، تعداد ارقام در یک عدد حاصل از اندازه گیری برابر تعداد ارقام با معنی است. برای مثال 1/85 متر یا 82/3 کیلو گرم سه رقم با معنی دارند، در حالی که 1609 چهار رقم با معنی دارد. در یک محاسبه باید بدانیم چند رقم با معنی در یک عدد وجود دارد.
استفاده از صفر برای تعیین بزرگی یک عدد کار را پیچیده می کند. صفرها همیشه رقم با معنی نیستند.
می توانیم چند قاعده بیان کنیم که در مورد همه اعداد به کار می رود:
الف) هرگاه صفر بین دو رقم باشد آن صفر، با معنی است. برای مثال 100/1K چهار رقم با معنی دارد و 0/305 سه رقم با معنی دارد.
ب) صفری که در آخر یک عدد باشد با معنی است. اگر این صفر در طرف راست ممیز باشد، با معنی است. مانند 10/91که چهار رقم با معنی دارد.
ج) صفری که فقط محل ممیز را نشان می دهد، با معنی نیست. برای مثال 0/0821 سه رقم با معنی دارد اما 1/082 چهار رقم با معنی دارد.
د) صفرهایی که بعد از یک عدد صحیح می آیند مبهم می باشند (در مقایسه با ب) . بدین ترتیب 1000m می تواند از یک تا چهار رقم با معنی داشته باشد.
علامت گذاری نمایی
در حل یک مسئله با استفاده از قاعده (د) در بالا می توانیم اعداد را به صورت حاصل ضرب عددی کوچک (بین 1 و 10) با توانی از 10 بیان کرد. بنابراین 400 چهار بار برابر 100 و 100 همان 102 می باشد. پس اگر عددی یک رقم با معنی داشته باشد می توانیم بنویسیم 102×4. اگر دو رقم با معنی داشته باشد می نویسیم 102×4/0 و اگر سه رقم با معنی داشته باشد می نویسیم 102×4/00 . این روش کارامد است زیرا طبق قاعدع (ب) صفرها در طرف راست ممیز همیشه با معنی هستند.
نکته: توان ده اثری بر روی ارقام با معنی ندارد و عدد کوچک (عددی بین 1 و 10 است) همیشه با یک رقم در سمت چپ ممیز نوشته می شود.
کاربرد دیگر علامت گذاری نمایی این است که نوشتن اعداد بسیار کوچک یا بسیار بزرگ را آسان می سازد. فرض کنید عدد حاصل از انداره گیری یازده میلیون (دو رقم با معنی) باشد. به جای این که 11,000,000 بنویسیمف می توانیم این عدد را به صورت 107×1/1 بنویسیم. از 7 استفاده می کنیم زیرا ممیز باید هفت رقم از عدد آخر به سمت چپ برود تا عدد 1/1 به دست آید یا چون 107 برابر 10 میلیون است پس 1/1 ضربدر ده میلیون می شود 11 میلیون.
یا فرض کنید عددی بسیار کوچک مانند 0/0000543 داریم. این عدد را به صورت 10-9×32/4 می نویسیم. از 9- استفاده می کنیم چون ممیز باید 9 رقم به سمت راست برود تا عدد 4/32 به دست آید. همین طور در مورد عدد 5/43 ×10-5 می دانیم که عدد 0/0000543 بوده است. ممیزها را 5 رقم به سمت راست حرکت داده ایم تا عدد 5/43 ×10-5 به دست آید.
استفاده از نماها برای تعیین تعداد ارقام صحیح در جواب ضرب و تقسیم عددهای بزرگ کار را بسیار آسان می کند. برای مثال اگر این عبارت
به صورت زیر تغییر کند
با یک نگاه می فهمیم که پاسخ تقریبی 107×2 می باشد.
به همین ترتیب وقتی عبارت
مثال:
کسر زیر را بدون استفاده از ماشین حساب حل کنید:
در حل این مسئله بهتر است که صورت کسر را به جای 1/76 ×10-3 به صورت 17/6 ×10-4 نشان دهیم تا پاسخ به جای
0/22×10-5 به صورت 6-10×2/2 به دست آید. اگر چه مقدار این دو عدد یکسان می باشد اما 6-10×2/2 ترجیح داده می شود.
محاسبه با استفاده از ارقام با معنی
دقت یک عدد را نمی توان با محاسبه بهتر کرد، زیرا اعداد از یک اندازه گیری به دست آمده اند . بنابراین وقتی محاسبه ای را انجام می دهید که اعداد آن از یک اندازه گیری به دست آمده اند نتیجه، دقیق تر از اندازه گیری های اولیه نیست. با عملیات ریاضی و استفاده از ارقام با معنی می توان نتیجه را به دست آورد.
- تعداد ارقام با معنی در نتیجه حاصل از یک ضرب یا تقسیم برابر عددی است که کمترین رقم با معنی را دارد. اگر بخواهیم عدد را گرد کنیم، این کار را به صورتی معمول انجام می دهیم. برای مثال، (2 رقم با معنی) 1/32×8/1 = 11
- وقتی جمع یا تفریق انجام می دهیم فقط ارقام (نه ارقام با معنی) سمت راست ممیز را در نظر می گیریم. نتیجه جمع یا تفریق باید تعداد رقم سمت راست ممیز عددی را داشته باشد که کمترین رقم را دارد. برای مثال
(یک رقم با معنی سمت راست ممیز دارد.) 1/327×18/1 =19/4
مثال:
تعداد ارقام معنی دار دو عدد 30.26 و 0.03026 برابر با چهار است. زیرا صفرهای چسبیده به ممیز فقط مکان ممیز را مشخص می کنند.
نکته:
برای رفع ابهام در مورد تعداد ارقام معنی دار، باید اعداد را به صورت نماد علمی نوشت، برای مثال، در مورد تعداد ارقام معنی دار عدد 4000 نمی توان به آسانی قضاوت کرد، مگر اینکه آن را به صورت علمی بنویسیم:
نکته:
اعداد قراردادی مانند جرم کربن 12، عدد 100 در محاسبات درصد و عدد 23 در عدد آووگادرو و ... به دلیل اینکه فاقد عدم قطعیت هستند، دارای بی نهایت رقم معنادار می باشند.
مرکز یادگیری سایت تبیان - مرجان سلیمانیان
منبع:
http://www.chemica.ir