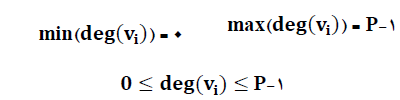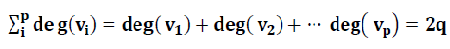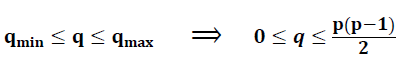گراف

یک گراف شامل دو مجموعه است ، مجموعه غیر تهی از گره ها یا رئوس (که با v نشان می دهند) و مجموعه ای از یال ها (که باE نشان می دهند).  گراف G با مجموعه رئوس v و یال های E را به صورتG(V,E)  نشان می دهند.

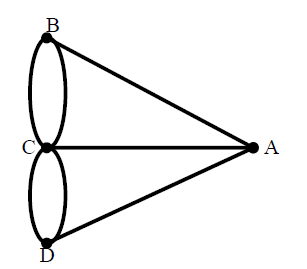
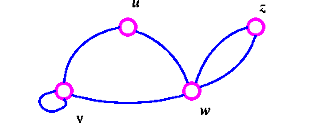
به عنوان مثال گراف زیر را در نظر بگیرید .مجموعه رئوس و یال های این گراف مشخص شده است .

 

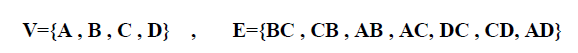
تعریف گراف ساده : گراف ساده گرافی است که بین هر دو راس آن حداکثر یک یال موجود باشد .(یعنی بین دو راس آن یا یک یال باشد یا یالی نباشد )
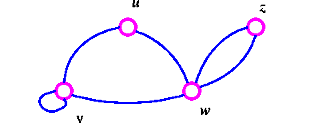
طوقه: اگر دو راس  ابتدا و انتهای یک یال  یکی باشد آن یال طوقه میباشد.(به عبارت دیگر از راسی شروع شده و به خودش باز گردد) .مانند یال متناظر با راس v  در شکل زیر:

گراف چند گانه : گرافی است که بین  دو راس آن  بیش از یک یال است .
مرتبه و اندازه گراف :به تعداد رئوس گراف مرتبه گراف (p) و به تعدداد یال های گراف اندازه گراف (q) می گویند .
گراف تهی : یک گراف تهی گرافی است که تنها شامل راس است و مجموعه یال های آن تهی است یعنی یالی ندارد.
 در واقع گرافی است که اندازه آن برابر صفر است .
گراف دو بخشی: گرافی که بتوان مجموعه راس های آن را به دو مجموعه X و Y افراز کرد، به طوری که هر یال از این گراف یک سر داخل X و سر دیگر آن در مجموعه Y باشد را  ،گراف دو بخشی می نامیم.
گراف جهت دار: یک گراف جهتدار گرافی است که جهت هر یال در آن تعیین شده است. در گراف جهت دار ترتیب رئوس در هر یال اهمیت دارد و یال ها با پیکان هایی از راس ابتدا به راس انتها رسم می شوند. در گراف غیرجهت دار می توان در هر دو جهت بین راس ها حرکت کرد و ترتیب راس های یال اهمیت ندارد.
تعریف درجه راس :به تعداد یال های گذرنده از یک راس ، درجه آن راس می گویند .درجه راس vi در گراف G  را با ( deg (vi نشان می دهند .
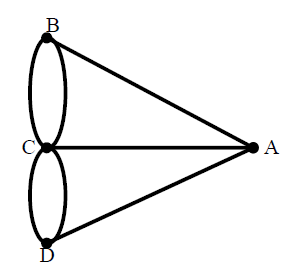
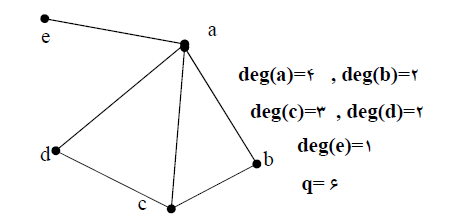
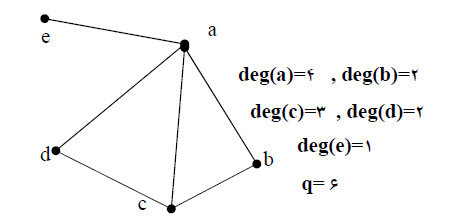
 مثال : در مثال زیر درجه رئوس و تعداد یال گراف مشخص شده است .

نکته :

قضیه  : مجموع درجات رئوس یک گراف برابر است با دو برابر یال های آن.

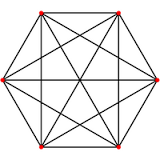
 گراف کامل : گراف کامل گراف ساده‌ای است که در آن هر رأس به تمامی راس‌های دیگر به وسیله یک یال متصل است. یک گراف کامل از مرتبه p ، با Kp  نشان داده می شوند . در یک گراف کامل درجه هر راس برابر است با p-1 . گراف کامل بیشترین یال ممکن را دارد  و دارای  p(p− 1)/2 یال است. بنابر این :

گراف منتظم: به گرافی گفته می‌شود که تمام رئوس آن درجه یکسانی دارند، گراف منتظمی که درجه هر رأس  آن r   باشد، گراف r-منتظم خوانده می‌شود. هر گراف تهی یك گراف 0 -منتظم و هر گراف n راسی كامل یك گراف 1 -n- منتظم است.  
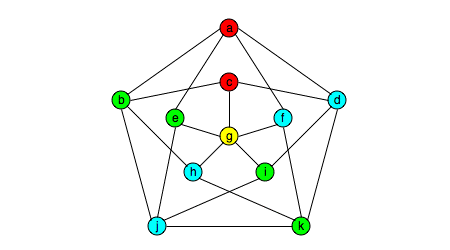
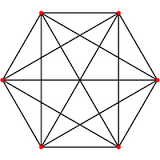
شکل زیر گراف کامل و 5-منتظم  می باشد .

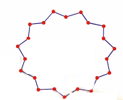
گراف دوری :هرگراف دوری یك گراف 2 -منتظم است.

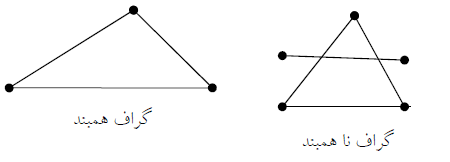
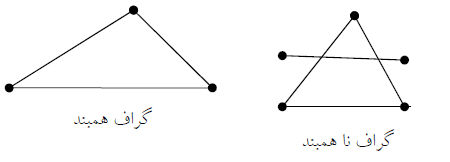
گراف همبند :  گرافی است که بین هر دو راس آن یک مسیر وجود داشته باشد .

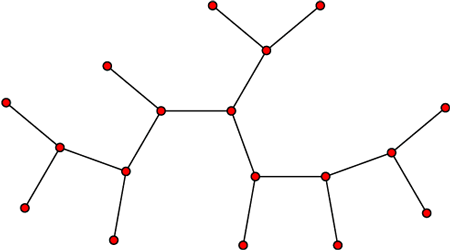
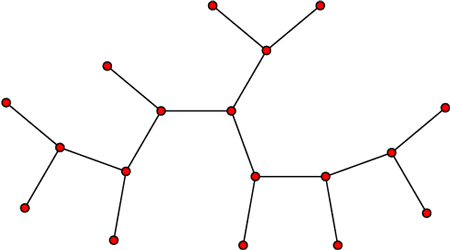
تعریف درخت : گراف همبند فاقد دور را درخت می نامند طوری که با اضافه کردن هر یال جدید دقیقا یک دور خواهیم داشت.
قضیه :اگر G درختی با p راس و q یال باشد  در آن صورت :    p=q+1

تهیه: پروین نظری-مرکز یادگیری سایت تبیان