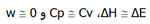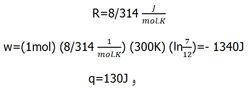مسائل ترمودینامیک (2)

مقدار تغییرات توابع حالت به مسیر پیموده شده بستگی ندارد و تنها به حالت اولیه و نهایی سیستم وابسته می باشد.

در مطلب قبل دانستید که چون مقدار فشار خارجی مخالف در کل انبساط برابر با یک اتمسفر است بنابر این، w= - (1atm) ΔV می باشد. (مطلب قبل را از این قسمت مرور کنید.)
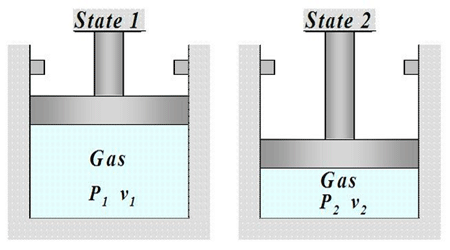
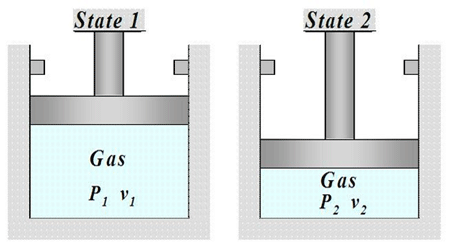
در ادامه راهنمایی هایی برای حل مسائل ترمودینامیک توجه کنید که گاز ابتدا، در حالت تعادل است، اما برداشتن وزنه ها از روی پیستون باعث از بین رفتن تعادل می شود. از این رو، گاز به طور خود به خود منبسط می شود تا به حالت تعادل جدید برسد. همچنین، امکان به وقوع پیوستن این تغییر توسط مسیری که سیستم همواره در حالت تعادل باشد، به طور نظری وجود دارد. چنین فرایندی را برگشت پذیر می نامند. وقتی یک فرایند برگشت پذیر رخ می دهد که وزنه ها به تدریج از روی پیستون برداشته شوند. اگر کل این فرایند در یک دمای ثابت، T، رخ دهد آنگاه w=nRTln V₁/V₂ می باشد.
که در این جا R ثابت گاز، n تعداد مول های گاز، T دمای مطلق (برحسب کلوین) و V₁ و V₂ به ترتیب حجم های اولیه و نهایی می باشند.

به طور خلاصه، w را می توان برای سه نوع فرایند محاسبه کرد:
1- حجم ثابت: w=0
2- تغییر حجم در مقابل یک فشار مخالف ثابت:w= - P_OPP ΔV
3- تغییر حجم برگشت پذیر:  w=nRTln V₁/V₂

مقدار q را می توان برای فرایندهای مشخصی از گازهای ایده آل نیز محاسبه کرد. یک فرایند هم دما فرایندی است که در دمای ثابت رخ می دهد. در مورد هر فرایند هم دمای یک گاز ایده آل، بنابر تعریف ΔV=0 و با توجه به قانون اول q= - w. بنابر این، اگر بتوانیم w را برای فرایند هم دما محاسبه کنیم، q را نیز می توانیم به دست آوریم. همچنین، می توان q را برای فرایندهایی که در آنها دما تغییر می کند محاسبه کرد، به شرط آن که حجم یا فشار ثابت باقی بماند. برای هر تغییر دما در حجم ثابت، qv=nCv ΔT که qv گرمای جذب شده در حجم ثابت، Cv ظرفیت گرمایی در حجم ثابت که مقدار آن برای یک مول گاز ایده آل برابر با 3/2R و n تعداد مول های گاز است. برای هر تغییر دمایی در فشار ثابت،qp= nCpΔT می باشد که qp گرمای جذب شده در فشار ثابت Cp ظرفیت گرمایی در فشار ثابت که مقدار آن برای یک مول گاز ایده آل برابر با 5/2R و n تعداد مول های گاز است.

 با توجه به قانون اول می توان ثابت کرد که ΔV= qv زیرا در حجم ثابت w=0 است.
حال در می یابیم که قانون اول برای تعریف یکی دیگر از توابع حالت H (آنتالپی) مناسب است، به طوری که ΔH= qp، زیرا بیشتر فرایندهای شیمیایی در فشار ثابت رخ می دهد. با توجه به قانون اول می توان نشان داد که ΔH= ΔE + Δ(PV)
در این جا Δ(PV)= P₂V₂ – P₁V₁  برای حالت 1 (حالت اولیه) و برای حالت 2 (حالت نهایی فرایند) مورد نظر می باشد.(در یک فرایند با فشار ثابت Δ(PV)= P ΔV)
بسیاری از این اندیشه ها را می توان برای سیستم هایی که تنها حاوی جامدات و مایعات هستند نیز به کار برد، با این تقریب که تغییرات حجم جامدات و مایعات طی فرایند قابل چشم پوشی است. از این رو می توان مانند زیر نوشت.

نکته: برای سیستم هایی که حاوی گازهای ایده آل هستند مانند فازهای متراکم، تنها باید تغییرات حجم را در نظر گرفت. همچنین، در مواردی که یک گاز ایده آل در یک فرایند تولید یا مصرف می شود، تنها باید تغییرات حجم گاز را مورد توجه قرار داد.

مثال: اگر در یک فرایند هم دما تغییری در مقدار گاز ایده آل به وجود آید، آنگاه با جایگزینی معادله گاز ایده آل در معادله  فوق 
  می باشد  ΔH= ΔE + RTΔn  به آسانی می توان نشان داد که ΔH= ΔE + Δ(PV)

 تغییر انرژی سیستمی را محاسبه کنید که 10 kJ گرما از محیط اطراف خود جذب می کند، در حالی که 8kJ کار روی سیستم انجام می شود.

قانون اول بیان می کند که تغییر انرژی برابر با مجموع گرمای جذب شده توسط سیستم و کار انجام شده روی سیستم است.
ΔE=q+w=10kJ+(-8kJ)=2kJ 

 یک مول از یک گاز ایده آل که حجمی برابر با 7L دارد، در دمای 300K به طور هم دما و برگشت پذیر تا حجم 12L منبسط می شود. ΔE، ΔH، q و w را محاسبه کنید.

چون فرایند هم دما می باشد پس ΔE=0، ΔH=0  و q=-w می باشد چون فرایند برگشت پذیر نیز هست در نتیجه w=nRTln V₁/V₂ می باشد.
برای محاسبه w داده ها را با واحدهای مناسب در این رابطه جایگزین می کنیم. به منظور به دست آوردن پاسخ برحسب ژول، از فرمول زیر استفاده می کنیم.

حجم گاز درون یک استوانه با یک پیستون بدون اصطکاک 20 لیتر و فشار خارجی 3 اتمسفر است. تعدادی از وزنه های روی پیستون را به طور ناگهانی بر می داریم، تا فشار خارجی به 1/5 اتمسفر برسد. بدین ترتیب، گاز به طور هم دما منبسط می شود تا به حالت تعادل جدید برسد. ΔE، ΔH، q و w را برای این تغییر حالت محاسبه کنید.
 ابتدا با جایگزین کردن مقادیر در قانون بویل، حجم نهایی را به دست می آوریم:
P₁V₁=P₂V₂, (3atm)(20L) = (1/5atm) (V₂), V₂=40L 
چون فرایند هم دما مباشد، پس ΔE=0 است. به آسانی می توان نشان داد که ΔH برای یک فرایند هم دمای گاز ایده آل نیز برابر با صفر است. چون در یک دمای معین P₁V₁=P₂V₂  ی باشد در نتیجه Δ(PV)=0 است و با توجه به معادله زیر:
 ΔH= ΔE+ Δ(PV)   می توان گفت ΔE=ΔH است.
اگر ΔE=0 باشد آنگاه با توجه به معادله q= - w, ΔE=q+w  است.
 برای محاسبه مقدار w، جزئیات مربوط به مسیر فرایند را بررسی می کنیم. حجم در مقابل فشار خارجی ثابت 1/5 atm در حال تغییر است. با استفاده از رابطه زیر بدست آورد.

به طور کلی، بهتر است که مقادیر ترمودینامیکی را برحسب ژول بیان کرد. ضریب تبدیل عبارت است از 1L.atm=101J
بنابراین، (w= -3010J)  
q= -(-3010J) = 3010J 
ادامه دارد ...
منبع:
http://library.sharif.ir

مسائل ترمودینامیک (1)
مسائل ترمودینامیک (3)

مرکز یادگیری سایت تبیان، مرجان سلیمانیان