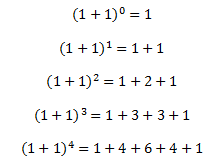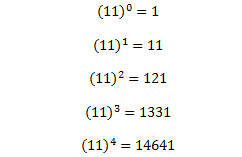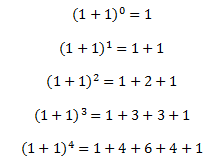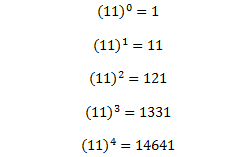چند کاربرد از مثلث خیام پاسکال

در این مقاله  شما با کاربرد های مثلث خیام پاسکال که در کتاب ریاضی دهم انسانی به آن اشاره شده است، آشنا می شوید و به ارتباط این مثلث با مثلث سرپینسکی پی خواهید برد.

تعریف :

مثلث خیام پاسکال در زبان ایتالیایی «مثلث تارتالیا» و در زبان چینی «مثلث یانگ هویی» نام گرفته است. عمر خیام ریاضی دان ایرانی نیز روشی جبری برای به دست آوردن ضرایب بسط دو جمله ای می کند.
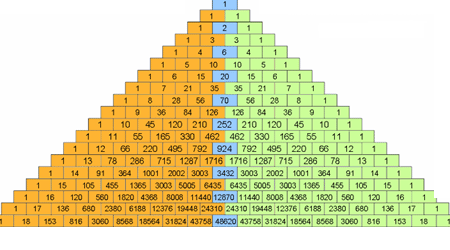
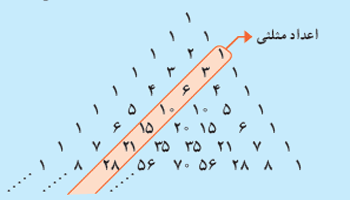
مثلث خیام پاسکال به شکل زیر تعریف شده است.   

کاربرد 1)

اگر به جای a و b عدد یک را بگذاریم چه اتفاقی می افتد ؟

 به عبارت دیگر ( 1+1 ) ⁿ برابر 2ⁿ است که با جمع اعداد سطر n+1 ام مثلث خیام پاسکال بدست می آید.

تمرین 1:

با استفاده از مثلث خیام پاسکال حاصل 2⁸ رابیابید ؟

کاربرد 2)

یک ارتباطی بین توان های مختلف عدد 11 و مثلث خیام پاسکال موجود است. توجه کنید :

همان طور که مشاهده می کنید برای محاسبه11ⁿ کافی ست اعداد سطر n+1 ام مثلث خیام پاسکال را کنار هم بنویسیم .

 

 تمرین 2:

با استفاده از مثلث خیام پاسکال حاصل   11⁶  را به دست آورید. ابتدا بگویید از کدام سطر باید استفاده کنید ؟

 

 

پاسخ تمرینات

پاسخ تمرین 1:

 

 

برای محاسبه 2⁸ باید اعداد سطر نهم مثلث خیام پاسکال را باهم جمع کنیم.

 

 

2⁸ =1+8+28+56+70+56+28+8+1=256

 

پاسخ تمرین 2:

کاربرد 3)

یکی دیگر از کاربرد های این مثلث در کتاب ریاضی دهم به وجود آمدن اعداد مثلثی در قطر مثلث خیام پاسکال می باشد. عددهای مثلثی همواره از 1 شروع می شوند و در مرحله ی اول 2 واحد به عدد اول اضافه می شود تا عدد دوم به دست آید. در مرحله بعد، 3 واحد به عدد قبلی اضافه می گردد و به این ترتیب الگوی عددی شکل می گیرد. در واقع اولین عدد مثلثی مساوی است با مجموع یک عدد از اعداد طبیعی، دومین معادل است با مجموع دو عدد از اعداد طبیعی، سومین معادل است با مجموع سه عدد از اعداد طبیعی و ... که بالاخره nامین عدد مثلثی معادل است با مجموع n عدد از اعداد طبیعی که مقدار این عدد معادل n(n+1)/2 خواهد بود.
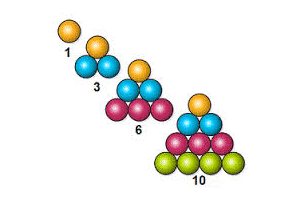
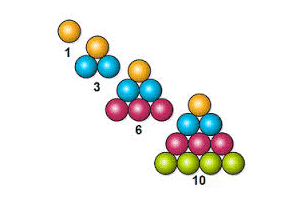
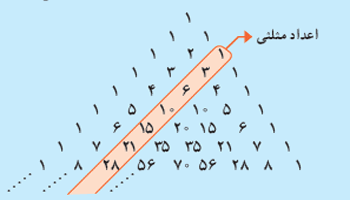
                                                                ... , 21 , 15 , 10 , 6 , 3 , 1

در مثلث خیام پاسکال اعداد روی ضلع  همگی یک هستند .قطر  اول برابر اعداد طبیعی  می باشد و قطر دوم برابر اعداد مثلثی هستند . می توانید این مورد را در شکل زیر مشاهده کنید .

 

مثلث سرپینسکی

مثلث سرپینسكی حاوی كپی هایی كوچك تر از خود است و می دانیم فراکتال شکل هندسی چند جزئی است که می‌توان آن را به قسمت هایی تقسیم کرد، به طوری که هر قسمت یک کپی از " کل " شکل باشد. 
بنابر این مثلث سرپینسکی نیز یک نوع فراکتال است که از مثلث خیام پاسکال براحتی می تواند حاصل شود.         


مرکز یادگیری سایت تبیان - تهیه: پروین نظری