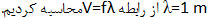بر هم نهی و تداخل

هدف:

وقتی دو یا چند موج به هم می رسند، ممکن است موج برایند آن ها به دلیل به دلیل تداخل یا برهم نهی امواج اولیه، کلی کاملا پیچیده داشته باشد. در این مطلب می خواهیم به ادامه مطلب "فاز در موج" و تداخل سازنده و ویرانگر اشاره کرده و همچنین شرایط لازم برای بر هم نهی امواج را بیان کنیم.

شرح درس:

مطلب را با تعریف کلمات تداخل و بر هم نهی شروع می کنیم.

بر هم نهی امواج:

وقتی دو یا چند موج به هم می رسند، اختلالی در وضعیت قرار گیری اولیه آن ها در محیط به وجود می آید. جمع دو یا چند موج در همان فضای اولیه امواج به هم رسیده را بر هم نهی امواج می نامند.

تداخل امواج:

نتیجه بر هم نهی امواج(جمع آن ها) تداخل است. بر هم نهی امواج، ترکیبی موجی شکل به وجود می آورد که باعث تداخل سازنده یا ویرانگر امواج اولیه می شود و می تواند در هر لحظه و مکانی کاملا متفاوت باشد.

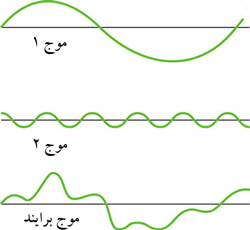
امواجی که در واقعیت مشاهده می کنیم، به سادگی تعریف های مطالب راجع به امواج یا موج های ساده روی آب نیستند! امواج ساده به وسیله نوسان هارمونیک ساده تولید می شوند و شکلی سینوسی دارند. اما امواج پیچیده تر، شکل های مختلفی دارند و عجیبند. بیشتر موج های ساده ای که با هم جمع می شوند، موج برایند کاملا پیچیده ای دارند اما خوشبختانه قانون جمع موج ها بسیار ساده است و دامنه موج ها به راحتی با هم جمع می شود.

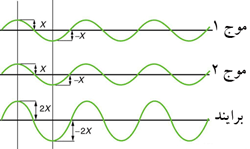
شکل زیر نشان دهنده برهم نهی امواج آب مختلف از چشمه های مختلف تولید موج است که موج برایند آن ها شکلی پیچیده دارد:

اگر دو موج مشابه در نقاط هم فاز خود با هم ترکیب شوند، دره ها و قله های آن ها دقیقا در یک امتداد قرار گرفته و این برهم نهی باعث تولید تداخل سازنده خالص می شود .دامنه موج منتجه، دو برابر دامنه هر کدام از موج های ترکیبی اولیه است؛ اما طول موج نهایی همان طول موج اولیه است.

همین اتفاق در مورد دو موج کاملا مشابه که نقاط غیر هم فاز آن ها با هم بر هم نهی می کنند، اتفاق می افتد. دو موج ترکیبی، تداخل ویرانگر خالص دارند. دامنه موج منتجه، صفر و امواج کاملا اثر هم را خنثی می کنند. اما همیشه بر هم نهی تمام امواج به این سادگی نیست. امواج همیشه شکل یکسانی ندارند.

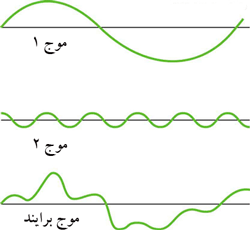
بر هم نهی بیشتر امواج، ترکیب هر دو تداخل سازنده و ویرانگر است و دامنه موج ترکیبی حاصل، نقطه به نقطه در دو یا چند موج با هم جمع جبری می شود و شکل موج نهایی پیچیده خواهد بود.

بیان ریاضی نقاط هم فاز و غیر هم فاز (فاز و طول موج):

1) حالت اول (نقاط هم فاز):

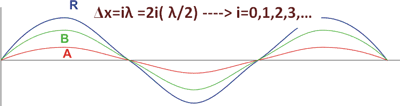
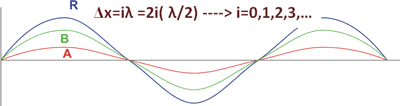
دو نقطه هم فاز از دو موج مشابه A و B را در نظر می گیریم. این دو نقطه دقیقا در یک حالت ارتعاشی در هر لحظه ای از زمان هستند و جابجایی و سرعت یکسان دارند. اختلاف فاز نقاط هم فاز همواره صفر رادیان یا مضارب زوجی از  رادیان است.

این دو نقطه طبق تعریف بالا تداخل سازنده دارند زیرا فاصله دو نقطه هم فاز موج های A و B به صورت مضرب صحیحی از طول موج است یا مضرب زوجی از نصف طول موج:

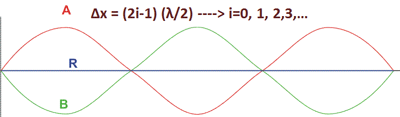
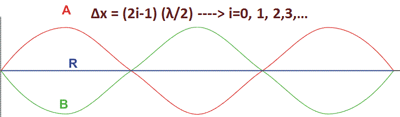
Δx=iλ =2i( λ/2) ----> i=0,1,2,3, ٦

موج برایند R را در شکل 4 مشاهده کنید که حاصل تداخل سازنده دو موج A و B است.

2) حالت دوم (نقاط غیر هم فاز):

نقاط موجود در موج های A و B تداخل ویرانگر دارند زیرا فاصله آن ها از همدیگر به صورت 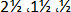  و ... است. یعنی این نقاط در هر لحظه ای ، ½ نوسان کامل خود از هم فاصله دارند. این امواج اثر هم را خنثی کرده و تداخل ویرانگر دارند. موج برایند این دو موج همان موج R است که هیچ دامنه یا طول موجی ندارد.

اختلاف مسیر دو موج شکل بالا مضرب فردی از λ/2 است و اختلاف فاز آن ها همواره مضارب فردی از   رادیان است.

Δx = (2i-1) (λ/2) ----> i=0, 1, 2,3, ٦

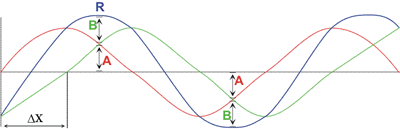
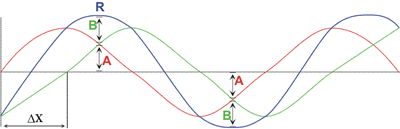
3) حالت سوم (حالت ترکیبی):

مانند شکل زیر برخی نقاط تداخل سازنده و برخی نقاط تداخل ویرانگر دارند.  موج برایند R نیز جمع جبری دو موج A و B است.

اختلاف مسیر بین دو نقطه در این موج ها میانگین طول موج است.

مثال1:
دو بلندگو با فرکانس های یکسان 340 هرتزی، موج هایی با دامنه و فاز مساوی از خود منتشر می کنند. اگر دامنه را با A نشان دهیم و بلندگوها 4 متر از همدیگر فاصله داشته باشند و رو به روی هم واقع شده باشند، به سوالات زیر پاسخ دهید:
(سرعت صوت در هوا 340 m/s است)

الف) طول موج صوت منتشر شده؟

ب) اگر کاهش دامنه موج صوتی هر بلندگو را در اثر فاصله با دیگری در نظر نگیریم، دامنه امواج صوتی دو بلندگو  دقیقا در حد وسط فاصله بین دو بلندگو چقدر است؟

ج) اگر کاهش دامنه موج صوتی هر بلندگو را در اثر فاصله با دیگری در نظر نگیریم، دامنه امواج صوتی دو بلندگو  در نیم متری از هر بلندگو چه قدر است؟

د) اگر کاهش دامنه موج صوتی هر بلندگو را در اثر فاصله با دیگری در نظر نگیریم، دامنه امواج صوتی دو بلندگو  در یک متری از هر بلندگو چه قدر است؟

جواب الف):

جواب ب)

چون حد وسط فاصله بین دو بلندگو 2 متر است و از قسمت الف می دانیم که 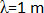، بنابراین اختلاف راه بین دو موج، مضرب صحیحی از طول موج است، در این قسمت تداخل سازنده بین دو موج داریم و در این فاصله، نقاط هم فازند؛ بنابراین دامنه موج برایند در این فاصله 2A خواهد بود.

جواب ج)

نیم متر یعنی مضرب فردی از نصف طول موج و غیر هم فاز بودن نقاط در این فاصله، بنابراین موج برایند در این نقطه هیچ دامنه ای نخواهد داشت.

جواب د)

همانند قسمت ب دقیقا فاصله نقاط مضرب صحیحی از طول موج است و بنابراین دامنه موج برایند در این فاصله 2A خواهد بود.

ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ

مثال 2:

دو منبع صوتی با دامنه های مساوی اما فرکانس های 800 هرتز و 804 هرتزی داریم.

الف) کم ترین فرکانس شنیده شده چه قدر است؟

ب) چه پدیده ای باعث کم شدن فرکانس می شود؟

جواب الف):

 اختلاف فرکانس دو منبع: 4 هرتز است. پس کم ترین فرکانس 4 هرتز خواهد بود.

جواب ب):

 پدیده ی ضرب آهنگ باعث کم شدن فرکانس می شود.

در مطالب بعدی به این موضوع بیشتر اشاره خواهیم کرد.