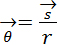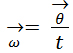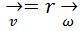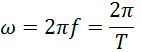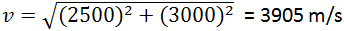حرکت دایره ای
هدف:
آشنایی با مفاهیم اولیه حرکت دایره ای، مثال ها و معادلات اولیه
شرح درس:
طبق قانون اول نیوتن اگر نیروی خالصی به اجسام در حال حرکت وارد نشود، اجسام به حرکت خود در یک خط مستقیم ادامه خواهند داد. اگر جسم در حال چرخیدن و سرعتش در حال تغییر باشد (حتی اگر این تغییر در جهت سرعت جسم باشد)، پس باید یک نیرویی بر این جسم در حال عمل کردن باشد.
در حرکت دایره ای، جسم در یک مسیر دایره مانند حرکت می کند؛ این به معنای آن است که جسم، قوسی از یک دایره (یا مسیر خمیده) را طی می کند.
حرکت دایره ای به دو دسته حرکت تقسیم می شود:
- حرکت دایره ای یکنواخت که در آن، جسم با سرعت ثابت حرکت می کند و فقط جهت سرعت در حال تغییر است.
- حرکت دایره ای غیر یکنواخت که در آن سرعت جسم (چه در اندازه و چه در جهت ) در حال تغییر است.
قوانین نیوتن برای حرکت دایره ای:
قانون اول نیوتن:
همانطور که در بالا اشاره شد، اگر جسمی در مسیر مستقیم حرکت می کند و سرعت آن ثابت است، هیچ نیرویی به آن وارد نخواهد شد. بنابراین جسمی که حرکت دایره ای دارد، چون سرعت آن (برای هر دو مورد یکنواخت و غیر یکنواخت) در حال تغییر است، پس نیرویی به این جسم وارد می شود که مسیر جسم را تغییر می دهد.
قانون دوم نیوتن:
جسمی که تحت تاثیر یک نیرو است، در جهت نیرو شتاب خواهد گرفت.
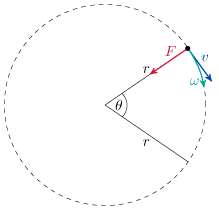
این عبارت به این معناست که نیروی وارد بر جسم نمی تواند مؤلفه هایی در جهت سرعت داشته باشد. برای همین، بردار نیرو در حرکت دایره ای، عمود بر بردار سرعت جسم است(یعنی به سمت مرکز دایره یا مسیر کروی که جسم در روی آن حرکت می کند).
پس:
شتاب در حرکت دایره ای یکنواخت طبق قانون دوم نیوتن F=ma عمود بر مسیر یا بردار سرعت است. در حرکت دایره ای غیر یکنواخت، یک مؤلفه غیر صفر در جهت حرکت وجود دارد برای همین شتاب در این حالت ،عمود بر مسیر حرکت نیست.
جابه جایی زاویه ای:
جسمی در یک حرکت دایره ای، قوسی از یک دایره را طی می کند. زاویه بین ابتدا و انتهای قوس (زاویه زیر قوس)، جا به جایی زاویه ای جسم نام دارد و به صورت زیر تعریف می شود:
که s طول قوس و r شعاع قوس است.
جا به جایی زاویه ای کمیتی برداری است ولی برای راحتی کار آن را به صورت نرده ای در نظر می گیرند.
واحد SI برای جا به جایی زاویه ای، رادیان است. یک رادیان، 180/π درجه است. جابجایی زاویه ای را می توان همان مسافت زاویه ای نامید.
سرعت زاویه ای:
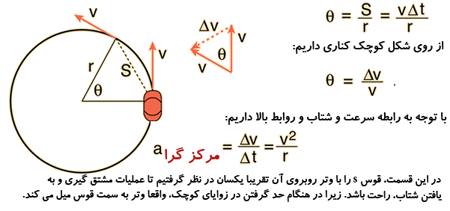
تغییرات جا به جایی زاویه ای را سرعت زاویه ای ω می نامیم ( یعنی تغییرات زاویه در واحد زمان) که کمیتی برداری است.
سرعت زاویه ای، آهنگ تغییر قوسی است که جسم در یک مسیر دایره ای طی می کند.
واحد SI برای سرعت زاویه ای، رادیان بر ثانیه است.
سرعت زاویه ای از طریق شکل زیر به سرعت خطی مماسی مربوط است:
دوره تناوب و فرکانس حرکت دایره ای:
از بحث بالا داریم:
از رابطه بین v و ω می توان گفت:v=2πr/T
حرکت دایره ای یکنواخت:
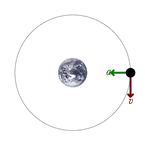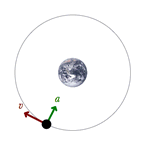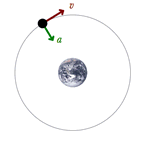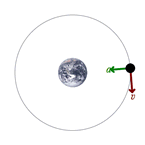
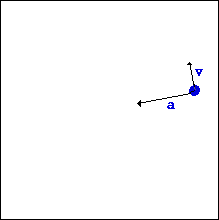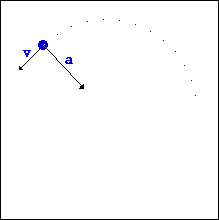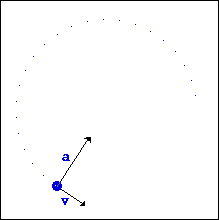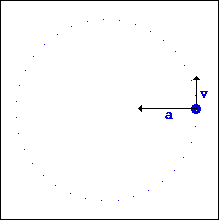
همانطور که قبلا هم اشاره شد، در حرکت دایره ای یکنواخت، سرعت جیم در حال حرکت در یک مسیر دایره ای ثابت است اما جهت سرعت به صورت ثابت در حال تغییر است. در این حرکت، بردار سرعت همواره مماس بر مسیر حرکت است.
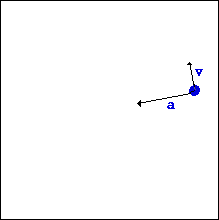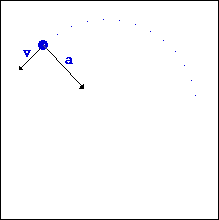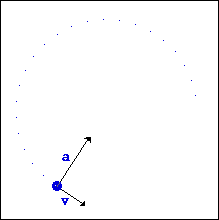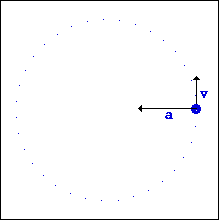
از آنجایی که جهت سرعت در حال تغییر است، جسمی که در مسیری دایره ای حرکت می کند، شتاب دارد. جهت بردار شتاب در حرکت دایره ای یکنواخت به سمت داخل دایره یا مسیر خمیده است.
طبق قانون دوم نیوتن، نیروی خالص وارد بر جسم نیز به سمت داخل مسیر دایره ای خواهد بود؛ به همین دلیل این نیرو را نیروی مرکز گرا نام گذاری کرده اند . بدون چنین نیروی مرکز گرایی، جسم به حرکت خود در مسیر خط راست ادامه می دهد. اما وجود این نیرو باعث می شود جسم همواره در یک مسیر دایره ای حرکت کند که بردار سرعت این جسم عمود بر بردار نیرو یا بردار شتاب است.
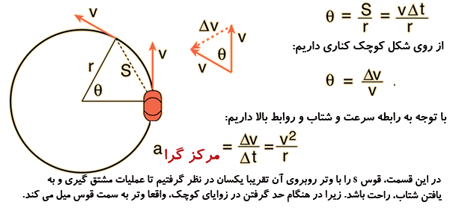
محاسبه شتاب مرکز گرا:
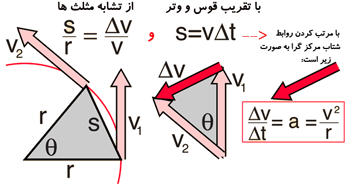
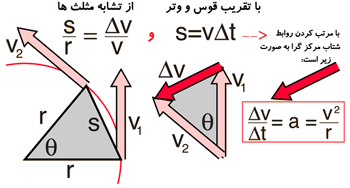
به شکل زیر نگاه کنید تا همه چیز برایتان مشخص شود:
از شتاب مرکز گرا نیز داریم: F=ma = m(v2/r)
به شکل زیر خوب دقت کنید:
اگر قسمتی از محیط دایره ای که توپ آن را طی می کند، برداریم، چه اتفاقی می افتد؟
بله درست است. توپ به حرکت خود در مسیر مستقیم ادامه می دهد زیرا مسیر دایروی آن از بین رفته و نیروی مرکز گرایی نیست تا آن را در روی دایره نگه دارد.
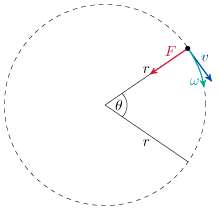
با توجه به شکل زیر می بینیم که نیروی مرکزگرا با مجذور سرعت متناسب است. اگر نیروی مرکزگرا تنها به دلیل نیروی اصطکاک سطح ایجاد شده باشد و اصطکاک ناچیز باشد، افزایش سرعت موجب لیزخوردن خیلی زیاد جسم در مسیر دایره ای خواهد بود؛ مثلا سر خوردن ماشین در انحنای جاده ای که در اثر بارش برف یا باران لیز شده است.
حال به فیلم زیر و تغییرات بزرگی بردار های حرکتی ماشین خوب نگاه کنید:
مثال(1):
یک ماشین مسابقه با سرعت مماسی ثابت 60 m/s یک مسیر دایره ای را در مدت 50 ثانیه دور می زند. بزرگی شتاب وارد بر ماشین را پیدا کنید.
حل:
از رابطهv=2πr/T داریم: r=Tv/2π
این r در رابطه a=v2/r جایگذاری می کنیم: a=7.5 m/s2
مثال(2):
خلبان ماهری یک مسیر دایره ای یکنواخت در آسمان اجرا می کند. سرعت اولیه هواپیما با رابطه v0=2500 i +3000 j به دست می آید. یک دقیقه بعد سرعت هواپیما به صورت v=-2500 i -3000 j در می آید. مقدار شتاب هواپیما را محاسبه کنید.
کاملا مشخص است که فقط جهت سرعت تغییر کرده و مقدار آن تغییری نکرده است. مقدار سرعت به صورت زیر است:
در حرکت دایره ای یکنواخت مقدار شتاب از رابطه a=v2/r به دست می آید و می دانیم که T=2πr/v :
از آن جایی که T دوره تناوب این حرکت است و از اطلاعات مسئله می توان فهمید که یک دقیقه طول می کشد تا جهت سرعت، معکوس شود(با توجه به علامت منفی در مولفه های بردار v)، پس دوره تناوبی حرکت، دو دقیقه (60 ثانیه)است:
بنابراین: a=204 m/s2
در مطلب بعد مثال های بیشتری حل خواهیم کرد.
مرکز یادگیری سایت تبیان - تهیه: خدیجه آلچالانلو
تنظیم: مریم فروزان کیا