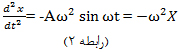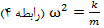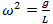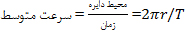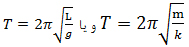حرکت آونگ (2)
هدف:
در ادامه مطلب "حرکت آونگ(1)" می خواهیم به معادلات حرکتی و روابط زمان تناوب و فرکانس و دامنه حرکتی آونگ بپردازیم.
شرح درس:
ابتدا باید فرض کنیم که فنر، طناب، نخ یا میله ای که گوی کوچک آونگ به آن متصل است، جرم ندارد.
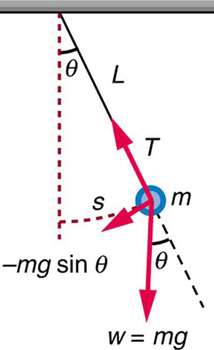
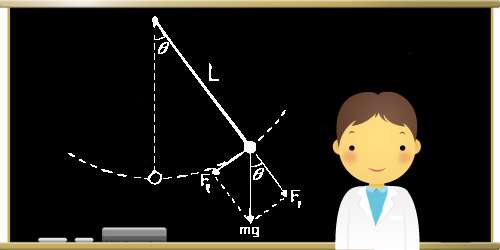
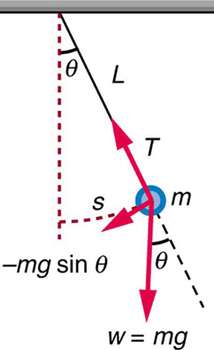
فرض می کنیم گوی جا به جایی کوچک s را انجام می دهد ( البته برای راحتی کار تصور می کنیم این جا به جایی گوی از نقطه تعادل خودش، به صورت منحنی نیست بلکه به صورت خطی است ). با توجه به برایند نیروهای وارد بر گوی، می بینیم که:
نیروی کشش طناب با مولفه عمودی نیروی وزن خنثی می شود:
T =mgcosθ
نیروی بازگرداننده گوی به حالت تعادل، طبق برایند نیروها با مؤلفه افقی نیروی وزن برابر است: mgsinθ=F
برای زاویه های خیلی کوچک ( یعنی کمتر از حدود 15 درجه ) می توان تقریبا sinθ را با خود θ یکی در نظر گرفت. بنابراین نیروی بازگرداننده F خواهد بود: F≈−mgθ
جا به جایی گوی نیز به طور مستقیم با θ متناسب است ( این یک نکته ریاضی کوچک، آموزنده و آسان است که بهتر است در این جا از آن استفاده کردهو به ذهن بسپاریم )، اگر θ بر حسب رادیان باشد: s=Lθ و θ=S/L
بنابراین برای زاویه های کوچک خواهیم داشت: F≈mgL/S
چون نیروی بازگرداننده گوی به حالت تعادل مانند نیروی بازگرداننده فنر به حالت سکون خود است، بنابراین:
F≈−kx ( رابطه 1)
که k ثابت فنر است و به جنس فنر بستگی دارد و x جابه جایی فنر از وضعیت تعادل را نشان می دهد. با مقایسه رابطه 1 و F≈mgL/S به این نتیجه می رسیم که اگر x و S را که هر دو به جا به جایی اشاره می کنند، یکی در نظر بگیریم، به رابطه k=mg/L (رابطه *) می رسیم .
این مطلب را تا همین جا در ذهن نگه دارید تا موضوع دیگری را هم بررسی کنیم. از مطلب "حرکت آونگ (1)" به یاد دارید که معادله حرکت نوسانگرها چیزی شبیه معادلهx = F(t) است؛ یعنی جابه جایی گوی از وضعیت تعادلی، تابعی از زمان است و البته به صورت سینوسی است. اگر بخواهیم معادله کلی حرکت نوسانگر ساده را بیان کنیم، خواهیم داشت:
X =A sin(ωt)
نگران نباشید! گیج شده اید؟ حتما سوال می کنید چرا ωt ؟
خود ω را بعدا معرفی خواهیم کرد. به دلیل این که می خواهیم بیان کنیم جابه جایی در هر لحظه از مسیر نوسانگر یا آونگ تابعی سینوسی از زمان است که ω در این معادله به عنوان یک کمیت وابسته به زمان عمل می کند و باید به یاد داشته باشیم که زمان نوسان به جنس و جرم اجزای نوسان مرتبط است. ( تصور کنید که نوسان آونگ و گوی متصل به آن با نوسان فنری که گویی به آن وصل شده است، متفاوت است؛ اگرچه هر دو یک حالت نوسانی را نشان می دهند و ویژگی های مشترک زیادی دارند ).
بسیار خوب! عجله نکنید، می خواهیم با آرامش به اصل ماجرا برسیم!
از معادله بالا دو بار نسبت به زمان مشتق بگیرید تا شتاب حرکت به دست آید:
رابطه 1 را با قانون دوم نیوتن یعنی F=ma مقایسه کنید:
-kx=ma و خواهیم داشت: a=-kx/m (رابطه 3)
حال رابطه 2 و 3 را با هم مقایسه کنید:
از مقایسه رابطه * و رابطه 2 هم می توان گفت که:
پس یک رابطه مهم دیگر را نیز پیدا کردیم.
لطفا باز هم صبور باشید تا مطلب دیگری را نیز بررسی کرده و به جمع بندی برسیم!
سرعت زاویه ای و رابطه آن با دوره تناوب:
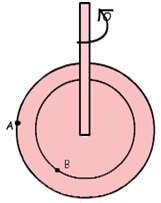
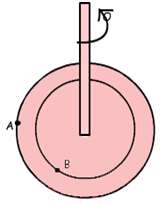
به شکل زیر خوب نگاه کنید. اگر میله عمودی یک چرخش داشته باشد، نقاط A و B هم یک چرخش خواهند داشت.
تعریف سرعت زاویه ای:
تغییرات جا به جایی زاویه ای یک جسم نوسانی در واحد خاصی از زمان( مثلا در یک ثانیه ). بنابراین واحد سرعت زاویه ای به صورت رادیان بر ثانیه باید باشد.
سرعت زاویه ای تمام نقاط روی محور عمودی شکل بالا که حرکت دایره ای انجام می دهند، با هم برابر خواهند بود؛ به دلیل این که تعداد چرخش ها در هر زمان یکی است.
اگر شعاع چرخش یا نوسان را r در نظر بگیریم و T دوره تناوب سیستم باشد، داریم:
(رابطه 5) ω=2π/T=2πf :پس
مثال:
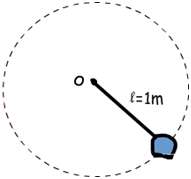
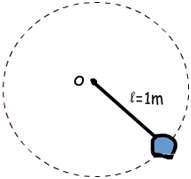
با توجه به شکل زیر اگر سنگ بسته شده به نخ، 6 چرخش در یک ثانیه انجام دهد، سرعت زاویه ای آن چقدر است؟
جواب:
اگر سنگ 6 چرخش در یک ثانیه داشته باشد، فرکانس آن 6 هرتز است و دوره تناوب آن یک ششم ثانیه است؛ پس سرعت زاویه ای آن ω=2π/T=2.3/(1/6s)=36radian/s است.
حال از رابطه 4 و رابطه 5 به این می رسیم که:
بنابراین دوره تناوب یک نوسان کننده مانند آونگ را به دست می آوریم. همان طور که می بینید، دوره تناوب به عواملی مانند شتاب ناشی از گرانش و طول آونگ یا فنر وابسته است.
مرکز یادگیری سایت تبیان - تهیه: خدیجه آلچالانلو
تنظیم: مریم فروزان کیا