
کاربردهای حرکت دایره ای
قانون دوم نیوتن
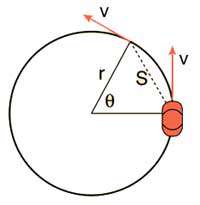
قانون دوم نیوتن بیان می کند که شتاب جسم با نیروی وارد بر آن رابطه ی مستقیم و با جرم جسم رابطه ی معکوس دارد. این قانون اغلب به شکل دو معادله بیان می شود:
Ftot = m×a
a = Ftot / m
قانون دوم نیوتن برای تحلیل موقعیت های مختلف فیزیکی استفاده می شود. ایده ی قانون این است که اگر هر موقعیت فیزیکی داده شده، به وسیله ی تک تک نیروهای وارد شده بر جسم، تحلیل شود، سپس باید برآیند نیروهای وارد شده بر جسم را محاسبه کرد. بنابراین نیروی کل باید با ضرب جرم در شتاب، برابر باشد. در نتیجه اگر جرم جسم و اندازه و جهت هر نیروی وارد شده بر جسم معلوم باشد، شتاب را می توان تعیین کرد. همچنین اندازه ی یک تک نیروی وارد بر جسم را می توان تعیین کرد، اگر جرم و شتاب جسم و اندازه ی بقیه ی نیروهای وارد بر جسم معلوم باشد. فرآیند تحلیل موقعیت های محتلف فیزیکی به منضور تعیین اطلاعات مجهول، به توانایی بیان آن موقعیت فیزیکی به وسیله ی نمودار جسم آزاد، بستگی دارد. نمودار جسم آزاد، نمودار برداری است که در آن اندازه و جهت نسبی همه ی نیروهای وارد بر جسم رسم می شود.
در این درس از مطالب درس قبل و اصول حرکت دایره ای برای تحلیل موقعیت های مختلف فیزیکی شامل حرکت اجسام در مسیر دایره ای یا منحنی، استفاده خواهیم کرد. معادلات رباضی و مفهوم نیروی مرکزی برای تحلیل ترن هوایی و دیگر وسایل سرگرم کننده ی موجود در پارک، حرکات ورزشی مختلف و دیگر پدیده های دنیای واقعی به کار می رود.
 |  |
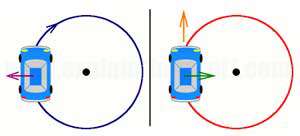
برای تصور این که چگونه برای تحلیل یک موقعیت فیزیکی، اصول حرکت دایره ای می تواند با قانون دوم نیوتن ترکیب شود، ماشینی را در نظر بگیرید که در سطحی صاف روی مسیر دایره ای افقی حرکت می کند. در شکل زیر ماشین در سمت چپ دایره رسم شده است. در نیروهای مرکزی، نیروی کل اعمال شده بر جسم، به سمت مرکز دایره است. چون در این شکل ماشین در سمت چپ دایره قرار گرفته است، نیروی کل به سمت راست است. در تحلیل این موقعیت باید توجه کنید که سه نیرو بر جسم وارد می شود، نیروی گرانش (به سمت پایین)، نیروی عکس العمل سطح (به سمت بالا) و نیروی اصطکاک (به سمت راست یا به سمت داخل). نیروی اصطکاک نیروی مرکزی لازم را برای حرکت ماشین روی مسیر دایره ای افقی تامین می کند. بدون وجود اصطکاک، چرخ های ماشین می چرخند ولی ماشین روی مسیر دایره ای حرکت نمی کند (مانند حرکت روی سطح یخی). این تحلیل منجر به نمودار جسم آزاد در سمت راست می شود. توجه کنید که هر نیرو با پیکانی که به جهت نیروی اعمال شده بر جسم اشاره می کند، نشان داده می شود. همچنین توجه کنید که هر نیرو نام گذاری می شود (گرانشF ، سطحF، اصطکاکF). این نوع تحلیل، اولین گام برای حل مسائل شامل قانون دوم نیوتن و حرکت دایره ای است.
حال دو مسئله ی زیر را که در مورد چرخش ماشین روی سطح افقی است، در نظر بگیرید:
مسئله ی 1:
یک ماشین 900 کیلوگرمی با سرعت 10 متر بر ثانیه، چرخش 180 درجه ای انجام می دهد. شعاع دایره ای که ماشین طی می کند، 25 متر است. تعیین کنید نیروی اصطکاک و ضریب اصطکاک اعمال شده بر ماشین را.
مسئله ی 2:
ضریب اصطکاکی که بر یک ماشین 900 کیلوگرمی اعمال می شود، 0.850 است. ماشین چرخش 180 درجه حول مسیری منحنی با شعاع 35 متر انجام می دهد. تعیین کنید ماکزیمم سرعتی را که ماشین می تواند با آن بچرخد.
مسئله ی 1 اطلاعات حرکتی (R,v) را داده و مقدار نیرو را خواسته است. برای حل این مسئله ابتدا باید شتاب و نیروی کل تعیین شوند. سپس مقدار نیروی خواسته شده با استفاده از نمودار جسم آزاد به دست می آید. مسئله ی 2 اطلاعات را درباره ی مقدار نیروهای اعمال شده بر جسم ( یا حداقل اطلاعاتی که به وسیله ی آن ها مقدار نیروها تعیین می شود. ) داده و مقدار ماکزیمم سرعت ماشین را خواسته است. برای حل این مسئله از مقدار نیروهای اعمال شده بر جسم برای تعیین نیروی کل و شتاب استفاده می شود. سپس به وسیله ی شتاب، ماکزیمم سرعت ماشین تعیین می شود. این دو مسئله، با استفاده از همان قوانین کلی حل می شوند. چون اطلاعات داده شده و خواسته شده در این دو مسئله متفاوت است، روش حل آن ها نیز کمی با هم فرق خواهد داشت.
روش پیشنهادی برای حل مسائل حرکت دایره ای
1- از شرح و توضیح شفاهی موقعیت فیزیکی نمودار جسم آزاد را رسم کنید. هر نیرو را با پیکان برداری نشان دهید و نیروها را نام گذاری کنید.
2- اطلاعات داده شده و خواسته شده را مشخص کنید. ( به وسیله ی متغیرها بیان کنید m=…,a=…,v=… و غیره )
3- اگر هر یک از نیروها با زاویه ای بر جسم اعمال شوند، از قواعد برداری برای تجزیه ی نیروها به نیروهای افقی و عمودی استفاده کنید.
4- مقدار نیروهای معلوم را مشخص کنید و آن ها را روی نمودار جسم آزاد بنویسید. (برای مثال اگر جرم معلوم باشد، گرانشF تعیین می شود. و به عنوان مثالی دیگر برای تعیین آسان یک یا چند نیروی وارد بر جسم در جهت عمودی، اگر شتاب عمودی وجود نداشته باشد، معلوم می شود که نیروهای عمودی و یا اجزای نیروها در تعادل هستند.)
5- از معادلات حرکت دایره ای برای تعیین هر یک از اطلاعات مجهول استفاده کنید. (برای مثال اگر سرعت و شعاع معلوم باشد، شتاب تعیین می شود. به عنوان مثالی دیگر اگر دوره ی تناوب و شعاع معلوم باشند، شتاب تعیین می شود.)
6- با استفاده از اطلاعات باقی مانده، اطلاعات خواسته شده را به دست آورید.
الف) اگر مسئله مقدار یک تک نیرو را بخواهد، از اطلاعات حرکتی (R,T,v) برای تعیین شتاب و نیروی کل استفاده کنید. سپس از نمودار جسم آزاد برای محاسبه ی مقدار آن نیروی خواسته شده استفاده کنید.
ب) اگر مسئله مقدار سرعت و شعاع را بخواهد، از مقادیر تمام نیروهای وارد بر جسم برای تعیین نیروی کل و شتاب استفاده کنید. سپس با استفاده از شتاب مقادیر سرعت و شعاع را تعیین کنید.
روش بالا برای حل مسائل حرکت دایره ای بسیار مفید است. با این وجود باید در نظر بگیرید که هر مسئله ی فیزیک با مسئله ی دیگر متفاوت است و برای حل هر یک از مسائل، هیچ فرمول جادویی وجود ندارد. استفاده از روش مناسب (شامل ایجاد نمودار جسم آزاد، مشخص کردن اطلاعات داده شده و خواسته شده و استفاده از معادلات موجود) برای حل چنین مسائلی، نیاز به تفکر و تحلیل مسائل را از بین نمی برد. به همین دلیل سعی کنید روش مناسبی را برای حل هر مسئله بیابید و مهارت های تحلیل مسائل را در خود تقویت کنید. اگر مسائل فیزیک، اثباتی، فرمول 5 مرحله ای یا استفاده از الگوریتم حفظی باشد، ما آن ها را "مسئله" نمی نامیم.

















