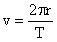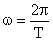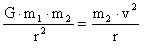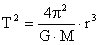محاسبه جرم مشتری – جلسه سوم

اصول حرکت دورانی و قانون کپلر

اهداف جلسه شامل اهداف رفتاری و آموزشی:

 زمان عملیاتی: 2 ساعت

 روند کار:

در این جلسه به بررسی قوانین حاکم بر حرکت اجرام تحت قانون گرانش می پردازیم. همان طور که می دانیم حرکت سیارات به دور خورشید (مثل مشتری و خود زمین) و نیز حرکت قمرها به دور سیارات از این قوانین تبعیت می کنند.

دو جرم m₁ و m₂ را در نظر بگیرید که به یکدیگر نیروی گرانش وارد می کنند، این دو جرم تحت شرایط خاصی می توانند به دور یکدیگر بچرخند : هنگامی که یکی از جرم ها خیلی بزرگ تر از دیگری باشد (مانند جرم خورشید و سیارات یا سیاره مشتری و قمرهایش)

جرم کوچک تر را در یک مدار به گرد جرم بزرگ تر (مرکزی) در نظر می گیریم. این مدار یک بیضی است، ولی در مورد اجرام منظومه شمسی، بیضی مدارها آن قدر به دایره نزدیک است که عملاً می توانیم از کشیدگی اندک مدار صرف نظر کنیم و مدار را دایره ای در نظر بگیریم.

بنابراین حالا جرم m₂ را داریم که در مداری دایره ای به دور جرم m₁ می گردد. دوره تناوب این گردش را T می نامیم. اگر جرم m₂ مسیرش را با سرعت v طی کند، یعنی: محیط دایره را در مدت زمان T با سرعت v می پیماید. پس می توانیم بنویسیم:

که در اینجا r شعاع مدار سیاره است.

در اینجا باید مفهوم دیگری را تعریف کنیم، با عنوان سرعت زاویه ای، که با مفهوم سرعت خطی متفاوت است. سرعت خطی (یا همان v) مسافتی است که جسم در واحد زمان طی می کند. ولی سرعت زاویه ای (یا  ω  ) زاویه ای است که جسم در واحد زمان طی می کند. از آنجا که محیط دایره است، سرعت زاویه ای در مدار چنین تعریف می شود:

قانون گرانش نیوتن: نیرویی که دو جسم به هم وارد می کنند، طبق قانون نیوتن از رابطه زیر پیروی می کند:

m₁ و m₂ جرم ذرات و r فاصله ی آنها از یکدیگر است.

هنگامی که  نیروی گرانش موجب چرخش دو جسم به دور یکدیگر می شود، می گوییم نیروی تحت عنوان جانب به مرکز به جرم دوم وارد می شود. البته نیروی جانب به مرکز تنها یک نیروی مجازی است که برای توصیف حرکت جسم دوم به آن نیاز داریم. مقدار این نیرو برابر با نیروی گرانش بین دو جسم است: F=mv²/r  در حقیقت این رابطه ایست که تعیین می کند جسمی که سرعت اولیه ی آن v است، (در صورت مشخص بودن جرم ها) باید در چه فاصله ای به دور جرم اول بگردد.

بنابراین می توانیم بنویسیم:

به این رابطه شکل نیوتنیقانون سوم کپلر می گویند. در این رابطه، همه ی کمیت ها بر حسب واحدهای SI گذاشته می شوند، یعنی دوره تناوب (T) بر حسب ثانیه، جرم بر حسب کیلوگرم و فاصله (r) بر حسب متر.

کپلر سالها قبل از نیوتن، با استفاده از داده های رصدی، توانسته بود برای سیارات منظومه شمسی این رابطه را به دست بیاورد که T²=r³ .  که البته در صورت بندی کپلر، T برحسب سال است و r بر حسب AU (یک AU یا یک واحد نجومی، فاصله ی زمین تا خورشید و  تقریباً برابر با 150 میلیون کیلومتر است.)

قانون کپلر با این اعداد، فقط برای اجرامی درست است که به دور خورشید می گردند (اگر در رابطه ی بالا، به جای M جرم خورشید را قرار دهیم)

با کمک قانون نیوتن و روابطی که گفته شد، این قانون تعمیم داده شد و حالا می توان از آن برای هر جرمی که به گرد هم می گردند استفاده کرد. از جمله برای مشتری (به عنوان جرم مرکزی) و قمرهایش!

خوب است با اعداد زیر برای هرکدام از روابط بالا مثال عددی برای دانش آموزان حل شود تا مفهوم برایشان ملموس تر شود.

(مثال هایی که مربوط به اجرام نجومی نباشد ولی برای تجسم نیروی گرانش مفید باشد هم خوب است. مثل نیروی گرانش بین دو دانش آموز در کلاس یا دو مورچه در فاصله ی 1cm  و  امثال این ها ... )

بخش پژوهش های دانش آموزی سایت تبیان

تنظیم: یگانه داودی

محاسبه جرم مشتری – جلسه اول
محاسبه جرم مشتری – جلسه دوم
محاسبه جرم مشتری – جلسه سوم
محاسبه جرم مشتری – جلسه چهارم