ساخت پل ماکارونی - جلسه اول
اهداف: آموزش مفاهیم اولیه و محاسبه نیروها در اعضای پل
مقدمه
ساخت پل ماکارونی خود به تنهایی موضوع جالبی است. روند کار پروژه به این صورت است که ابتدا مفاهیم مربوط به پل ( پل خرپایی) را معرفی می کنیم. جلسات اولیه پروژه را به تعریف مفاهیم و نحوه محاسبات نیرو در اعضای پل اختصاص داده ایم. برای ساخت یک پل ماکارونی باید بدانیم که کدام اعضا نیروی بیشتری را تحمل می کنند و کدام اعضا نیروی کمتری تا اعضای تحت نیروی بیشتر را مقاوم تر در نظر بگیریم در متن پروژه مثال های مختلفی از نحوه ی محاسبه نیروهای اعضای پل آمده شده است.
یک رشته ماکارونی، وقتی تحت کشش قرار می گیرد، مقاومت بیشتری دارد نسبت به وقتی که تحت فشار قرار می گیرد. یعنی حالت (ب) نشان می دهد که ماکارونی در کشش و فشار تحت یک نیروی برابر، در حالت فشار زودتر می شکند. در نتیجه باید بدانیم کدام اعضای پل دارای نیروی کششی و کدام اعضا دارای نیروی فشاری هستند که برای اعضایی که تحت فشار هستند از مصالح با ضمانت بیشتر یا از تعداد بیشتری ماکارونی استفاده کرد.
در جلسات بعدی که جلسات عملی کار است، نمونه هایی از پل ماکارونی آورده شده است که دانش آموزان می توانند شروع به ساخت این نمونه ها کنند. همچنین در CD ضمیمه پروژه، عکس هایی از اینترنت آورده شده است که انواع مختلفی از پل های ماکارونی ساخته شده را نشان می دهد. می توان از این نمونه ها نیز استفاده نمود.
در ساخت پل باید تمامی ضوابط اجرایی که در متن پروژه آورده شده رعایت شود.
پیشنهاد: با توجه به دیدگاه استاد، دانش آموزان می توانند همزمان با فراگیری مفاهیم و محاسبات نمونه های ساده ای از انواع پل را نیز بسازند تا در حین ساخت بهتر با مفاهیم آشنا شوند و نیز جذابیت پروژه حفظ شود.
نکاتی که در همه جلسات باید رعایت شود، فراهم بودن وسایل و مصالح مورد نیاز برای پروژه است.
تعریف مفاهیم مربوط به بردارها
تعریف نیرو و بردار نیرو
نیرو نماینده کنش یک جسم بر روی جسم دیگر است و به طور کلی با نقطه اثر، بزرگی و راستایش مشخص می شود. نیروهایی که بر یک ذره معین وارد می شود نقطه اثر مشترکی دارند.
بزرگی نیرو با عددی از یکاها مشخص می شود. یکاهای SI که مهندس ها برای اندازه گیری بزرگی نیرو بکار می برند عبارتند از: نیوتن (N) و کیلو نیوتن (KN) راستای نیرو را خط اثر و جهت نیرو مشخص می کند.
جمع بردارها
نیروها از قواعد معمول جمع در حساب و جبر پیروی نمی کنند. به عنوان مثال حاصل جمع دو نیروی عمود بر هم 4 نیوتنی و 3 نیوتنی 5N می شود نه 7N.
√(42+32 )=5
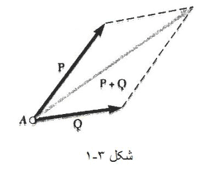
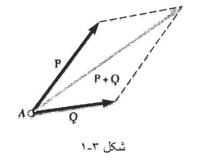
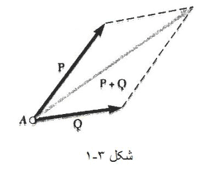
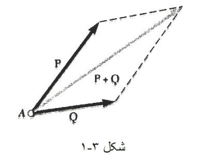
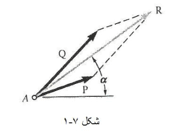
بردارها، بنا به تعریف، طبق قانون متوازی الاضلاع به هم افزوده می شوند. بنابراین مجموع دو بردار P و Q را می شود با اتصال آن ها به نقطه ای مثل A و رسم متوازی الاضلاع نیروها بدست آورد، به طوری که P و Q دو ضلع مجاور این متوازی الاضلاع باشند مطابق شکل زیر:
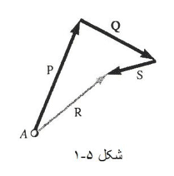
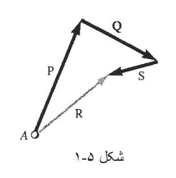
برآیند چند نیروی هم رأس
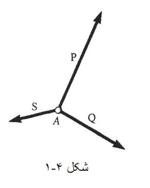
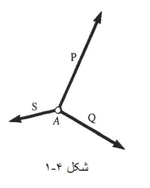
یک ذره A را در نظر بگیرید که به آن چند تا نیروی هم صفحه (یعنی نیروهایی واقع در یک صفحه) اثر می کنند.
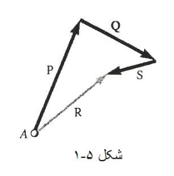
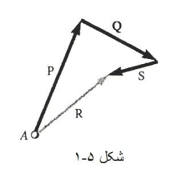
چون همه این نیروها از A می گذرند. آن ها را اصطلاحا هم رأس می گویند. مجموع بردارهای نماینده نیروهای وارد بر A را می شود با استفاده از قاعده چند ضلعی بدست آورد. از آنجا که استفاده از قاعده ی چند ضلعی عملا معادل با کاربرد مکرر قانون متوازی الاضلاع است، پس بردار R که به این ترتیب بدست می آید، نماینده برآیند نیروهای هم رأس وارد بر A خواهد بود. یعنی نیرویی که به تنهایی بر ذره A همان اثر نیروهای اولیه را دارد.
تجزیه یک نیرو به مولفه های آن
تا این جا دیدیم که دو یا چند نیروی وارد بر یک ذره را می شود به یک تک نیرو تبدیل کرد که همان اثر را بر روی ذره دارد. بر عکس هر تک نیروی F را که به یک ذره اثر می کند می شود تبدیل به دو یا چند نیرو کرد که (با هم) همان اثر را بر ذره می گذارند. این نیروها را مولفه های نیروی اصلی F می گویند و به فرآیند جایگزینی آن ها به جای F می گویند: تجزیه نیروی F به مولفه ها
Fx: مولفه نیروی F در راستای محور x
Fy: مولفه نیروی F در راستای محور y
چگونه مساله حل کنیم؟
برای حل مساله طبق مراحل زیر عمل کنید:
1- ببینید چه نیروهایی وارد می شوند و کدام نیرو، نیروی برآیند است. بد نیست که معادله برداری وابستگی نیروها را بنویسید مثلا برای شکل 3-1: R=P+Q-
2- یک متوازی الاضلاع بکشید که دو ضلع مجاورش همان دو نیروی مورد نظر (Q,R) و قطر متوازی الاضلاع برابر با برآیند این دو نیرو (R) باشند.(شکل 3-1)
یا از قاعده مثلث استفاده کنید. یعنی نیروها را به طریق سر به دم رسم کنید و برای پیدا کردن برآیندشان دم اولین بردار را به سر دومین بردار وصل کنید. مطابق شکل زیر:
3- همه مقادیر عددی را نشان بدهید. یکی از مثلث های دو نیمه متوازی الاضلاع یا مثلث حاصل از قاعده مثلث را در نظر بگیرید و همه ابعاد را، اعم از ضلع و زاویه روی آن نشان دهید و اندازه های مجهول را به روش ترسیمی یا مثلثاتی بدست آورید. اگر از روش مثلثاتی استفاده می کنید، یادتان باشد که در صورت معلوم بودن دو ضلع و زاویه بین آن ها، اول قانون کسینوس ها را به کار ببرید و اگر یک ضلع و دو زاویه معلوم بود از قانون سینوس ها استفاده کنید.
مسئله نمونه 1:
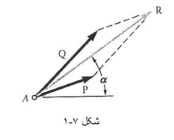
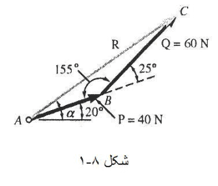
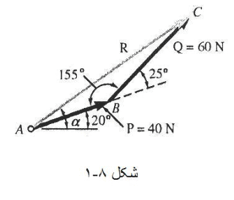
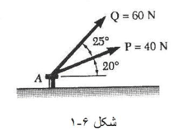
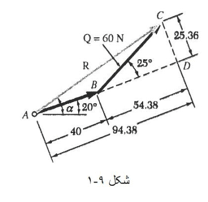
دو نیروی P و Q مطابق شکل به پیچ A اثر می کنند برآیند آن ها را تعیین کنید.
حل:
الف) حل ترسیمی: متوازی الاضلاع نیروها را با دو ضلع P و Q به مقیاس درست رسم می کنیم و بعد بزرگی و راستای برآیند را اندازه می گیریم، به این ترتیب نتیجه می شود که
از قاعده مثلث هم می توانیم استفاده کنیم. نیروهای P و Q را به شیوه سر به دم رسم کنید و مجددا بزرگی و راستای برآیند آن ها را اندازه می گیریم. (به عهده دانش آموز)
ب) حل مثلثاتی: باز هم از قاعده مثلث استفاده می کنیم؛ دو ضلع و زاویه بین آن ها معلوم است؛ با استفاده از قانون کسینوس ها داریم:
R² = P² + Q² - 2PQ cos β
R² = (40N)² + (60N)² - 2(40N)(60N) cos 155°
R = 97.73 N
حالا با به کاربردن قانون سینوس ها می نویسیم:
sin A ⁄ Q = sin B / R sin A ⁄ 60N = sin 155° / 97.73 1
از حل معادله (1) بر حسب SinA ، نتیجه می شود:
sin A = (60) sin 155° / 97.73 N
با استفاده از ماشین حساب ابتدا خارج قسمت کسر، بعد آرک سینوس آن را محاسبه می کنیم که نتیجه می شود:
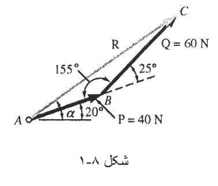
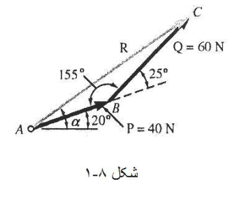
A= 15.04° α = 20° + A = 35.04°
پاسخ ها را فقط تا سه رقم با معنی ثبت می کنیم.
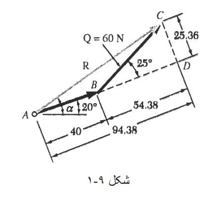
حل دیگر مثلثاتی: مثلث قائم الزاویه BCD را رسم و مقادیر زیر را محاسبه می کنیم:
CD = (60N) sin25° = 25.36 N
BD = (60N) cos25° = 54.38 N
حال با استفاده از مثلث ACD، داریم:
tan A = 25.3 N / 94.38 N A= 15.04°
R = 25.36 / sinA R= 97.73 N
باز هم به نتیجه قبلی می رسیم:
α = 20° + A = 35.04°
R = 97.7N , α = 35°
توجه: مساله نمونه 2 به عنوان تمرین به دانش آموزان داده شود.
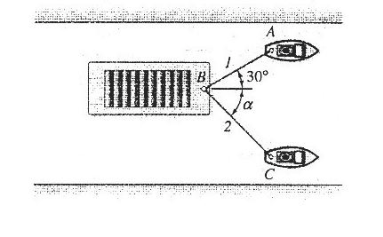
مسئله نمونه 2:
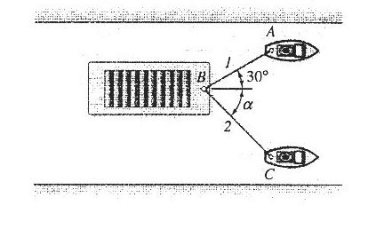
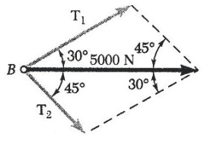
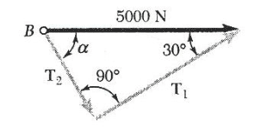
قایق B توسط دو یدک کش A و C کشیده می شود. اگر برآیند نیروهایی که یدک کش ها وارد می کنند 5000N و در امتداد محور قایق باشد،
الف) کشش در هر یک از طناب ها را تعیین کنید. α =45°
ب) مقدار a را طوری تعیین کنید که کشش در طناب 2 حداقل باشد.
حل:
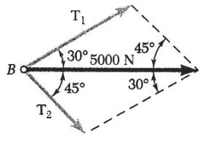
الف) حل ترسیمی: از قانون متوازی الاضلاع استفاده می کنیم؛ قطر متوازی الاضلاع (یا برآیند نیروها) معلوم و برابر با 5000N به طرف راست است، اضلاع آن را موازی با طناب ها رسم می کنیم. اگر شکل را به مقیاس درست رسم کنیم. با اندازه گیری این مقدارها را بدست می آوریم.
T1=3700N T2=2600N
حل مثلثاتی: می توانیم از قاعده مثلث استفاده کنیم. توجه می کنیم که این مثلث نمایانگر نیمی از متوازی الاضلاع پایین است. با استفاده از قانون سینوس ها می نویسیم:
T1 / sin 45° = T2 / sin 30° = 5000N / sin 105°
ابتدا با ماشین حساب خارج قسمت کسر آخر را حساب می کنیم و نتیجه را به حافظه می دهیم. سپس این مقدار را به ترتیب در sin 45° وsin 30° ضرب می کنیم که نتیجه می شود:
T1=3660N T2=2590N
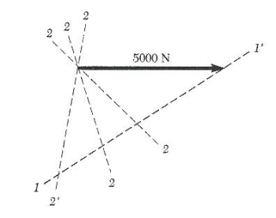
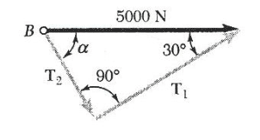
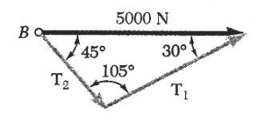
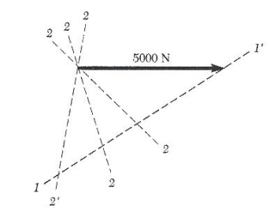
ب) مقدار a برای این که T2 حداقل باشد. برای این که a را طوری تعیین کنیم که کشش در طناب 2 حداقل باشد، باز هم از قاعده مثلث استفاده می کنیم. در شکل (13-1) خط 1-1 امتداد معلوم کشش T1 است. T2 می تواند راستاهای مختلفی داشته باشد که در شکل با خطوط 2-2 نشان داده شده اند.
می بینیم که مقدار T2 وقتی حداقل می شود که T1 و T2 بر هم عمود باشند. مقدار حداقل T2 برابر است با:
T2 = (5000N) sin 30° = 2500 N
و مقدارهای متناظر T1و α برابرند با:
T2 = (5000N) cos 30° = 4330 N
α = 90° - 30° = 60°
منابع مطالعه: برای مطالعه بیشتر و حل مسائل بیشتر می توانید به کتاب های با موضوع استاتیک مراجعه کنید. همچنین اینجا کلیک کنید تا اطلاعاتتان بیشتر شود.
مطالب مرتبط:
ساخت پل ماکارونی - جلسه پنجم
بخش پژوهش های دانش آموزی - تنظیم: فاطمه گودرزی