آشنایی با بهینه سازی
درجه سختی: متوسط
خلاصه: در این پروژه با بهینه سازی و روشهای حل مسائل بهینه سازی (به صورت مختصر) با بیان یک مثال ساده آشنا خواهید شد.
اهداف: آشنایی با بهینه سازی و ضرورت آن
وسائل مورد نیاز:
کاغذ و قلم
بهینهسازی چیست؟
1: یک مسئلهی بهینهسازی چه جور مسئلهای است؟
ما در روز کارهای بسیاری انجام میدهیم، چیزهایی میخوریم، چیزهایی یاد میگیریم، به جاهای مختلفی میرویم، از وسایل مختلفی استفاده میکنیم و ... و البته سعی ما این است که تمامی این کارها را به «بهترین» نحو ممکن انجام دهیم. مثلا اگر میخواهیم خرید کنیم، بهترین یعنی باکیفیتترین محصولات را بخریم. یا مثلا اگر میخواهیم درسی را بخوانیم، آن را به بهترین شکل، یعنی به شکلی که توانایی حل مسائل مختلف آن درس را به ما بدهد، یاد بگیریم. (واقعا این کار را میکنید؟!) واضح است که برای انجامدادن هر کار راههای زیادی وجود دارد.
مثلا فرض کنید که مادرتان یک فهرست خرید به شما داده و خواستهاست که تمامی آنها را تهیه کنید. انتخابهای زیادی برای خرید وجود دارد، اینکه اول چه کالاهایی خریداری شوند و بعد اینکه هر کالا را از کدام مغازه بخریم. اما مسئلهای که وجود دارد این است که، چگونه خرید کنیم که هم «کمترین» پول را بپردازیم و هم خرید «کمترین» زمان ممکن طول بکشد. به عبارت دیگر چگونه خرید کنیم که خرید ما «بهترین» یا «بهینه» باشد. به چنین مسئلهای، یک «مسئلهی بهینهسازی» میگوییم. در یک مسئلهی بهینهسازی با یک سری «متغیر» سروکار داریم. مثلا در مسئلهی خریدکردن، ترتیب خرید کالاها و همینطور مغازههایی که کالاها را میفروشند، متغیرها هستند. یعنی میتوانیم از بین حالتهای مختلف، انتخاب کنیم که به ترتیب چه کالایی را از کدام مغازه بخریم. «جواب بهینه» در واقع دسته متغیرهایی است که «هدف» را تأمین میکند. در مثال خرید، جواب بهینه ترتیب خرید کالاها و مغازههای مربوط به آنها است، به نحوی که هدف یعنی کمترین زمان خرید و کمترین پول پراختشده را تأمین کند.
معمولا سعی میکنیم که هدف را به صورت «تابعی» از متغیرهای مسئله بنویسیم. به این تابع «تابع هدف» میگوییم. بدین ترتیب در یک مسئلهی بهینهسازی، سعی میکنیم که مقدار بهینه را برای تابع هدف به دست بیاوریم. و نقطهای که در آن مقدار تابع هدف بهینه میشود، جواب بهینهی مسئله است.
اهداف مسئلههای بهینهسازی معمولا دستیابی به کمترین هزینه یا کمترین زمان صرفشده، یا بیشترین راحتی و رضایت برای کاربر یا مشتری است. مثالهای زیادی از این دست وجود دارند. سعی کنید برای هر مورد هدف و متغیرها را تشخیص دهید:
پیداکردن بهترین جنس و ابعاد برای صندلی تا بیشترین عمر را داشتهباشد؛ پیداکردن بهترین زمانبندی حرکت قطارهای مترو تا مسافران کمترین زمان معطل شوند؛ پیداکردن بهترین اندازهها برای یک لیوان تا لیوان کمترین قیمت را داشتهباشد؛ پیداکردن بهترین نوع اتومبیل تا راننده بیشترین احساس راحتی را داشتهباشد و ...
مسئلهی پیداکردن بهترین جواب وقتی اهمیت بیشتری پیدا میکند که دست ما کاملا باز نباشد. مثلا فرض کنید که کسی میخواهد یک اتومبیل بخرد؛ اگر او شخص ثروتمندی باشد، بدون فوت وقت بهترین و احتمالا گرانترین اتومبیل موجود را خواهد خرید. ولی اگر مثلا 10 میلیون تومان پول داشته باشد، چه باید بکند؟ او سعی میکند که «بهترین» اتومبیل را با این «قید» که قیمت آن از 10 میلیون تومان بیشتر نشود، بخرد. تقریبا تمامی مسئلههای بهینهسازی که در عمل به آنها برمیخوریم، یک یا چند قید دارند. بدون وجود قید خیلی از مسئلههای بهینهسازی بیمعنا میشوند، مثلا در مورد مسئلهی پیداکردن بهترین جنس و ابعاد برای صندلی تا بیشترین عمر را داشته باشد، واضح است که هرچه از مواد مستحکمتری استفاده کنیم و هرچه قدر ضخامت بدن و دستهها را بیشتر کنیم، صندلی بیشتر عمر میکند، ولی در این صورت قیمت آن آنقدر زیاد میشود که دیگر کسی آن را نخواهد خرید! بنابراین با این قید مواجهیم که قیمت مثلا از 30 هزار تومان بیشتر نشود.
هریک از مثالهای بالا میتوانند به ترتیب زیر قید داشته باشند، که به مسئلههای واقعی نزدیکترند:
پیداکردن بهترین جنس و ابعاد برای صندلی تا بیشترین عمر را داشته باشد، با این قید که قیمت آن از 30 هزار تومان بیشتر نشود؛ پیداکردن بهترین زمانبندی حرکت قطارهای مترو تا مسافران کمترین زمان معطل شوند، با این قید که سرعت حرکت قطارها برای ایمنی مثلا از 60 کیلومتر در ساعت بیشتر نشود؛ پیداکردن بهترین اندازهها برای یک لیوان تا لیوان کمترین قیمت را داشتهباشد، با این قید که حداقل 150 سیسی حجم داشتهباشد؛ پیداکردن بهترین نوع اتومبیل تا راننده بیشترین احساس راحتی را داشتهباشد، با این قید که قیمت آن از 10 میلیون تومان بیشتر نباشد و ...
2: مسئلهی پیداکردن بهترین مسیر برای رفتوآمد از خانه به مدرسه
تا اینجا حرفها همه کلی بودند و شاید قدری مبهم. برای فهم خوب یک مفهوم باید مسئله حل کنیم. در اینجا یک مسئلهی بهینهسازی را که قید هم دارد، «تعریف» میکنیم. تعریف یک مسئله یعنی اینکه تعیین کنیم: «متغیرهای مسئله چه هستند؟ قید مسئله چیست؟ هدف چیست؟» و هدف را به صورت تابعی از متغیرها بنویسیم، که به آن «تابع هدف» میگوییم. مسئلهی تعیینکردن بهترین راه برای رفتوآمد از خانه به مدرسه را به صورت زیر میتوان تعریفکرد:
یک دانشآموز میخواهد از خانه به مدرسه برود و بعد بازگردد، اما او تعداد مشخصی کار، مثلا n-1 کار دیگر هم در این بین دارد، یعنی باید به n-1 جا سر بزند. بدین ترتیب دانشآموز باید از خانه خارج شود، با در نظر گرفتن مدرسه به n جای مشخص شهر برود و سرانجام به خانه بازگردد. مکان جغرافیایی خانه، مدرسه و نقاط دیگر مشخص است. بنابراین این دانشآموز از خانه خارج میشود و از تمام n نقطه میگذرد، و البته مقداری از وقت خود را در مدرسه خواهدبود، مسئله این است که کوتاهترین مسیر برای عبور از همهی نقاط چیست؟
برای راحتی نام این مسئله را «مسئلهی دانشآموز پرکار» میگذاریم. مثلا به شکل زیر توجه کنید؛ دانشآموز میخواهد از خانه (محل 0) به مدرسه (محل 1) برود، یک کتاب را هم میخواهد به کتابخانهی محله (محل 2) پس بدهد، با همکلاسیها میخواهد یک سری هم به پارک (محل 3) بزند، یک خطکش هم می خواهد از لوازمالتحریری (محل 4) بخرد، یک نامه پست (محل 5) کند و البته برای خانه از بقالی سر کوچه (محل 6) چیزهایی بخرد. فعلا فرض میکنیم که فرقی نمیکند که این کارها بعد یا قبل از مدرسه انجام شود:


یعنی دانشآموز از خانه به نقطهی 4 حرکت میکند، آنگاه به ترتیب، به مکانهای 3، 6، 2، 5 و 1 میرود و سپس به خانه برمیگردد. شکل بالا در واقع یک «جواب ممکن» مسئله است. ما قصد داریم که بهترین جواب را از میان جوابهای ممکن به دست بیاوریم.
- قید مسئله
مسئلهی «دانش آموز پرکار» بسیار شبیه به مسئلهی «فروشندهی دورهگرد» است. این مسئله در زیر شرح داده شدهاست:
در منطقهای که n شهر وجود دارد، و بین همهی شهرها جاده وجود دارد و فاصلهی هر دو شهر مشخص است، فروشندهای دورهگرد قصد دارد محصولات خود را در تمام این n شهر عرضهکند و به فروش برساند. به این منظور قصد دارد از یک شهر حرکت خود را آغاز کرده و از تمام این شهرها بگذرد و به شهر اول بازگردد، بهطوریکه از هیچ شهری دو بار عبور نکند. حال مسئله این است که کوتاهترین مسیر ممکن کدام است؟
اگر گفتید که فرق این دو مسئله چیست؟
مسئلهی دانش آموز پرکار در واقع یک «قید» دارد، در حالیکه مسئلهی فروشندهی دورهگرد قید ندارد. قید مسئلهی اول این است که نقطهی شروع و پایان حرکت دانشآموز معلوم است. یعنی اگر به شکل 2 نگاه کنید، میبینید که مرحلهی اول و آخر جواب همهی جواب های ممکن نقطهی 0 یا همان خانه است، که با رنگ دیگر نشان داده شدهاست.
- تابع هدف
تابع هدف در واقع طول مسیر حرکت است که میخواهیم «کمینهی» آن را پیدا کنیم. برای محاسبهی طول مسیر انتخابشده، باید روی مسیر از خانه شروع به حرکت کرد و فاصلهی هر دو مکان متوالی را با استفاده از رابطه به دست آورد و همه را با هم جمع کرد.
3: روشهای حل یک مسئلهی بهینهسازی
سادهترین روش حل این است که از روش «سعی و خطا» استفاده کنیم. یعنی مثلا برای مسئلهی دانشآموز پرکار تمامی مسیرهای ممکن را تکتک تشکیل بدهیم و تابع هدف را برایشان محاسبه کنیم. بعد جوابها را با هم مقایسه کنیم. برای این کار، برای n مکان (n-1)! مسیر وجود دارد. یعنی برای مثلا 25 کار (اگر دانش آموزی اینقدر کار داشته باشد!) حدود 120،000 میلیارد مسیر ممکن وجود دارد. واضح است که استفاده از چنین روشی حتی برای پر سرعتترین کامپیوتر ها غیرممکن است.
یک روش معمول برای تعیین نقطهی بهینهی یک تابع، این است که از تابع بر حسب متغیرها مشتق بگیریم. جایی که مشتق یک تابع صفر شود، یک نقطهی بهینه داریم. این روش در درس حسابان ارائه میشود و اگر خودتان مطالعهی فوقبرنامه ریاضی داشتهباشید، احتمالا این روش را مطالعه کردهاید. بسیاری از روشهای بهینهسازی از همین اصل استفاده میکنند. در این دسته از روشها همهی مراحل کاملا از پیش تعیین شدهاند و هیچگونه «عدد تصادفی» در حل مسئله وجود ندارد. به این روشها، «روش های تَعَینی» میگوییم. برای بسیاری از مسئلهها استفاده از روشهای تعینی مقرونبهصرفه نیست؛ چون حل خیلی سخت میشود و یا آنکه حل بسیار وقتگیر خواهدبود. بعضی از مسئلهها را هم اصلا نمیتوان به روش مشتقگیری حل کرد. برای مثال همین مسئلهی دانشآموز پرکار را نمیتوان به این روش حل کرد. (چرا؟)
در مقابلِ روشهای تعینی، روشهایی وجود دارند که در آنها از اعداد تصادفی استفاده میکنیم. این روشها قدری شبیه به روش سعی و خطا هستند، یعنی به صورت تصادفی شروع به جستجو در میان جوابهای ممکن میکنیم. اما در این روشها نشانهها و راهنماییهایی وجود دارند تا متوجه شویم که به جواب بهینه نزدیک شدهایم. برای همین به این روشها، روشهای «راهنَمونی» میگوییم. روشهای راهنمونی مختلفی وجود دارند. این روشها عمدتا از فرایندهایی که در طبیعت اتفاق میافتد، اقتباس شدهاند. برای مثال روشهای زیر را ببینید:
• کلونی مورچهها: الهام گرفتهشده از روش یافتن کوتاهترین مسیر برای رسیدن به غذا توسط مورچهها.
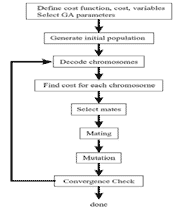
• الگوریتم ژنتیک: الهام گرفتهشده از پدیدهی تکامل در طبیعت.
• روش بازپخت شبیه سازی شده: الهام گرفتهشده از فرایند خنکشدن مواد مذاب و تشکیل مادهی جامد.
حال سعی کنید مسأله دانش آموز پر کار را از روش سعی و خطا حل نمایید! پس از این کار درباره الگوریتم ژنتیک مطالعه نموده و سعی کنید مسأله دانش آموز پر کار را بوسیله الگوریتم ژنتیک حل نمایید.
کدام روش سریع تر جواب داد؟
تحقیق کنید: بهینه سازی در چه جاهایی کاربرد دارد؟ سایر روشهای بهینه سازی کدامند؟
منابع مطالعه: کتاب الگوریتم ژنتیک و بهینه سازی مهندسی سید موسی حسینی- نشر گوتتبرگ