اندازه گیری زاویه بر حسب رادیان

معمولاً جا به جایی زاویه‌ای را با سه واحد مختلف اندازه گیری می‌كنند. اولین آن "درجه" است كه به عنوان   محیط دایره می‌باشد. واحد دیگر اندازه گیری زاویه عبارت از "چرخش" است.

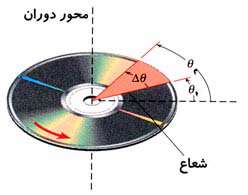
به طوری كه یك چرخش (rev) برابر زاویه كل دایره می‌باشد. مفیدترین واحد برای زاویه (از دیدگاه علمی)  "رادیان" (rad) است. در شكل مقابل چگونگی تعریف رادیان را مشاهده می‌كنید.

در شكل مقابل به نقطه p توجّه كنید.

این نقطه به عنوان شروع فرض می‌شود. به طوری كه _٠ و

جا به جایی زاویه‌ای برابر مقدار زیر خواهد بود.

نقطه p مسافت s را بر روی محیط دایره به شعاع r می‌پیماید.

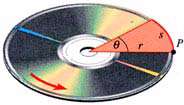
طبق تعریف، زاویه  بر حسب رادیان برابر است با:

اندازه زاویه بر حسب رادیان عبارت از نسبت دو طول می‌باشد (مثلاً متر/ متر)، بنابراین از دیدگاه ریاضی، رادیان عددی بی واحد می‌باشد. همچنین انتخاب واحدهای مختلف برای اندازه گیری طول اثری بر مقدار آن ندارد.

برای تبدیل واحد رادیان به درجه و بالعكس كافی است به این نكته توجّه شود كه طول كمان یك دایره كامل به شعاع r برابر  است. بنابراین اندازه زاویه یك دایره كامل بر حسب رادیان برابر با:

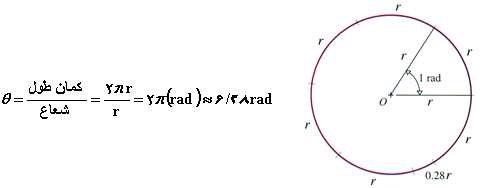
اندازه (rad) متناظر با ٣٦٠^٠ خواهد بود یا یك رادیان برابر:

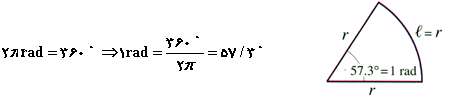
اندازه گیری زاویه بر حسب رادیان بسیار مفید و مناسب می‌باشد زیرا به وسیله ضرب زاویه () در طول شعاع r می‌توان طول كمان s را به دست آورد. ( s =r )

به مثال زیر توجّه كنید.

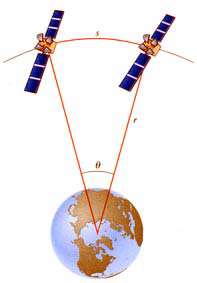
ماهواره‌ای بر روی دایره‌ای به شعاع:

r = 4/23 * 10⁷m  به دور زمین می‌چرخد. مدار چرخش بر صفحه استوا منطبق است.

ماهواره در دو موقعیت به اختلاف زاویه مشاهده می‌شود. فاصله s بین دو ماهواره را (به شكل توجّه كنید) به دست آورید.

راهنمایی:

از آنجا كه شعاع r و زاویه  مشخص است بنابراین طول كمان s را می‌توان به راحتی به دست آورد. (s =r).

اما بایستی دقت نمود كه  بر حسب رادیان باشد.

حل:

هر درجه معادل  رادیان است بنابراین برای تبدیل واحد داریم:

طول كمان s نیز برابر است با:

مرکز یادگیری سایت تبیان - تهیه: محسنی

تنظیم:‌ مریم فروزان کیا