حركت چرخشی و جا به جایی زاویه ای

حركت به سه شكل كلی قابل تحقق است:

جا به جایی

چرخش

مركب
اگر حركت طوری باشد كه هر خط رسم شده بین دو نقطه از جسم پس از جا به جایی نیز موازی نقاط متناظر اوّلیه اش باشد آنگاه حركت را جا به جایی مینامند.
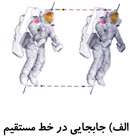
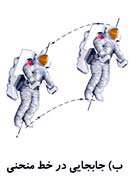
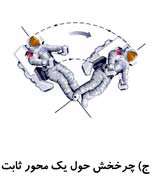
در نهایت، حركتی كه هم چرخشی باشد و هم جا به جایی، به عنوان حركت مركب شناخته میشود.
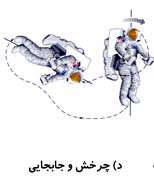
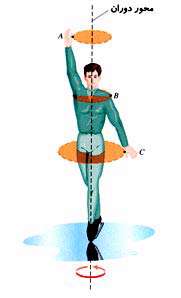
ساده ترین حركت چرخشی، حركت نقاط واقع بر روی یك جسم در یك مسیر دایروی میباشد. به عنوان مثال در شكل زیر، ما مسیرهای دایروی كه توسط نقاط B، A و C (بر روی یك اسكیت باز) طی میشود را مشاهده میكنیم.
خط واصل بین مراكز مسیرهای دایروی به عنوان محور دوران شناخته میشود.
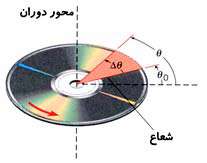
زاویهای كه یك جسم حول محور دوران میچرخد جا به جایی زاویهای نام دارد. در شكل مقابل لوح فشردهای (CD) در حال دوران است و جا به جایی زاویهای برای آن تعیین شده است.
در این شكل محور دوران از وسط CD عبور میكند و جا به جایی زاویهای بر روی صفحه CD واقع است.
در این شكل خطی بر روی صفحه CD رسم شده كه بر محور دوران عمود است.
شعاع از موقعیت زاویهای اوّلیه ٠ به موقعیت زاویهای نهایی
به موقعیت زاویهای نهایی  حركت میكند. در این فرآیند شعاع، زاویهای برابر با مقدار زیر را جاروب میكند. یعنی:
حركت میكند. در این فرآیند شعاع، زاویهای برابر با مقدار زیر را جاروب میكند. یعنی:

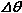 جا به جایی زاویهای میباشد.
جا به جایی زاویهای میباشد.یك جسم ممكن است در جهت ساعتگرد یا پاد ساعتگرد بچرخد، طبق قرار داد جهت پاد ساعتگرد به عنوان مثبت و جهت ساعتگرد به عنوان منفی شناخته میشود.
وقتی یك جسم حول یك محور ثابت دوران كند جا به جایی زاویه ای 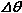 به عنوان مقدار زاویهای كه بوسیله شعاع (خط واصل بین هر نقطه واقع بر جسم و عمود بر محور جاروب میگردد) تعریف میشود.
به عنوان مقدار زاویهای كه بوسیله شعاع (خط واصل بین هر نقطه واقع بر جسم و عمود بر محور جاروب میگردد) تعریف میشود.

اگر با مفهوم رادیان (rad) كم آشنا هستید به شما اكیداً توصیه میشود، مبحث بعدی ما را حتماً دنبال کنید. با ما همراه باشید.
مرکز یادگیری سایت تبیان - تهیه: محسنی
تنظیم: مریم فروزان کیا

















