حركت درفضای دو و سه بعدی
تا كنون ما حركتهایی را بررسی نمودیم كه در راستای خط مستقیم صورت میپذیرفت. (مثل حركت مورچه بر محور x در شكل زیر) اما در حالت كلی ممكن است حركت در فضای دو بعدی (حركت لاك پشت) یا سه بعدی (زنبور) صورت گیرد.

اگر چه ما میتوانیم حركت در بعد دو و سه را با حركت در فضای یك بعدی تقریب بزنیم اما اكنون درصدد آن هستیم كه این حركتها را در حالت عمومی بررسی نماییم.
بردار جابجایی
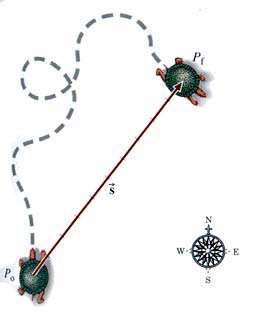
فرض كنید یك لاك پشت كوچك را بر روی یك تكه كاغذ در نقطه p٠ قرار دهید و آن را برای مدتی ترك كنید.
وقتی باز میگردید، لاك پشت در موقعیت جدید Pf كشف میشود! ما هیچ اطلاعاتی از مسیر حركت آن نداریم، اما میدانیم كه لاك پشت حركت كرده است.
جا به جایی لاك پشت عبارت از خط مستقیمی است كه از نقطه p٠ شروع شده و به نقطه Pf ختم میگردد.
بنابراین هم طول و هم جهت دارد. مسیر پر پیچ و خم حركت خزنده به نقطهای به فاصله ١٠cm در جهت شمال شرق ختم گشته است. پس میتوان جا به جایی لاك پشت را با یك بردار نشان داد.
جا به جایی یك جسم از نقطه شروع p٠ ، برداری است كه از آن نقطه شروع شده و به موقعیتی كه جسم قرار دارد ختم میشود.
جا به جایی اغلب مهم است. به عنوان مثال فوتبالیستی را در نظر بگیرید كه درصدد پاس دادن به فرد دیگری است. بدیهی است برای وی فاصله و جهت آن فرد مهم است.
بردار جا به جایی را با نماد  نشان میدهیم. نمادی كه از ابتدای كلمه فضای بین دو جسم (space) اقتباس شده است.
نشان میدهیم. نمادی كه از ابتدای كلمه فضای بین دو جسم (space) اقتباس شده است.
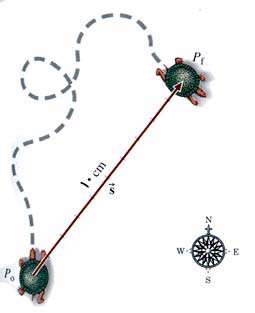
در شكل زیر بردار  به وسیله پیكانی به طول ١٠cm در راستای شمال شرق نشان داده شده است
به وسیله پیكانی به طول ١٠cm در راستای شمال شرق نشان داده شده است
(اگر رسم برداری به طول واقعی ١٠cm مقدور نبود آنگاه برای سادگی آن را به مقیاس (كوچكتر) رسم میكنیم.)
لاك پشتی را در نظر بگیرید كه در یك حركت جدید ٣cm به شرقp٠ برود (جا به جایی  ). سپس به اندازه ٩٠٠ دور زده و در راستای شمال ٤cm برود و به نقطه نهایی pf برسد (جا به جایی ٢
). سپس به اندازه ٩٠٠ دور زده و در راستای شمال ٤cm برود و به نقطه نهایی pf برسد (جا به جایی ٢ ).
).
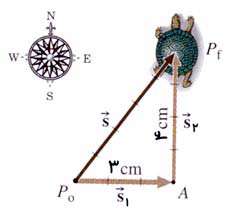
جا به جایی كل نسبت به مبداء (p٠ ) عبارت از  میباشد. بدیهی است طول
میباشد. بدیهی است طول  برابر خواهد بود با:
برابر خواهد بود با:

و راستای بردار  در جهت شمال شرق میباشد.
در جهت شمال شرق میباشد.
البته دقت كنید كه لزوماً مفهوم جا به جایی فقط در فضای دو و سه بعدی مطرح نمیشود، بلكه میتوان این مفهوم را در فضای یك بعد نیز تعریف نمود. به فیلم زیر توجّه كنید.
مرکز یادگیری سایت تبیان - تهیه: محسنی
تنظیم: مریم فروزان کیا

















