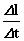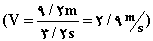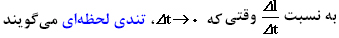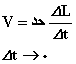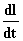تندی لحظهای
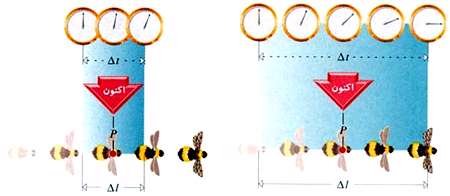
در مبحث قبل توضیح دادیم تندی متوسط از رابطه زیر به دست می آید:
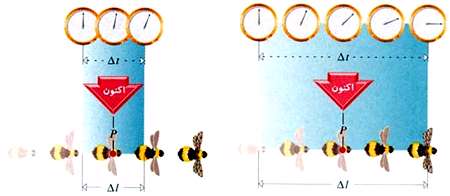
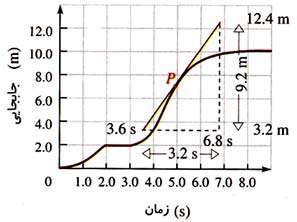
همین طور گفتیم با كوچكتر كردن  دقت محاسبه تندی لحظه بهتر خواهد شد. مجدداً به شكلهای زیر دقت كنید.
دقت محاسبه تندی لحظه بهتر خواهد شد. مجدداً به شكلهای زیر دقت كنید.
حال فرض كنید كه زنبور از نقطهای به فاصله 0/000005m قبل از p تا نقطهای به فاصله 0/000005m بعد از p در مدت 0/0000002s حركت كند. تندی متوسط در این بازه زمانی برابر این مقدار زیر خواهد بود.
این مقدار تندی متوسط بسیار دقیق و به لحظه t=٥s نزدیك میباشد. اما این دقیقاً تندی لحظهای در نقطه p نیست. ولی بسیار به آن نزدیك است.
با تقلیل دادن  و
و 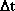 ما به تندی در لحظه p نزدیكتر میشویم. البته یك بیان هندسی برای به دست آوردن تندی لحظهای در نقطه p وجود دارد.
ما به تندی در لحظه p نزدیكتر میشویم. البته یك بیان هندسی برای به دست آوردن تندی لحظهای در نقطه p وجود دارد.
وقتی 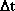 كوچك و كوچكتر انتخاب میشود،
كوچك و كوچكتر انتخاب میشود،  نیز كوچك میگردد و نسبت:
نیز كوچك میگردد و نسبت:
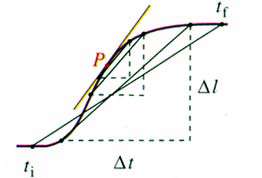
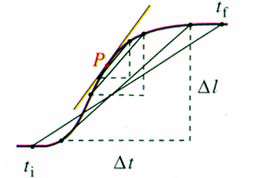
به شیب نمودار در نقطه p نزدیك تر میگردد. شیب نمودار 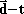 در هر نقطه همان شیب خط مماس به منحنی در آن نقطه میباشد. (شكل زیر)
در هر نقطه همان شیب خط مماس به منحنی در آن نقطه میباشد. (شكل زیر)
شیب (دقیق) در نقطه p همان تندی لحظهای است. با دقت در شكل زیر درمییابیم كه زنبور با تندی برابر مقدار زیر از مقابل بینی شما عبور میكند یعنی:
نكته كلیدی در اینجا این است كه با كوچكتر كردن 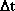 متناظراً
متناظراً  كوچك میشود اما نسبت
كوچك میشود اما نسبت 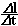 به یك مقدار معین نزدیك میگردد.
به یك مقدار معین نزدیك میگردد.
توجّه داشته باشید كه حاصل تقسیم یك عدد ریز بر یك عدد ریز دیگر لزوماً حاصلش ریز نخواهد بود!
و داریم:
از این پس وقتی از كلمه "تندی" استفاده میكنیم منظور همان تندی لحظهای است.
دقت كنید كه مقدار 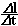 وقتی محاسبه میشود كه
وقتی محاسبه میشود كه 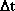 به صفر نزدیك شود نه اینکه
به صفر نزدیك شود نه اینکه 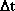 صفر گردد. اینكه تندی متوسط در بازه زمانی صفر محاسبه شود بی معنی است.
صفر گردد. اینكه تندی متوسط در بازه زمانی صفر محاسبه شود بی معنی است.
هیچ جنبندهای در ٠=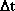 نمیتواند حركت داشته باشد. بنابراین تندی متوسط در ٠=
نمیتواند حركت داشته باشد. بنابراین تندی متوسط در ٠=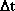 بی معنی است. این موضوع برای قرن ها مورد بحث و تیز بینی فیزیكدان ها قرار داشت.
بی معنی است. این موضوع برای قرن ها مورد بحث و تیز بینی فیزیكدان ها قرار داشت.
ما از V و Vav در بازه زمانی مشخص 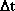 صحبت میكنیم و وقتی تندی در لحظهای خاص مد نظر باشد آنگاه
صحبت میكنیم و وقتی تندی در لحظهای خاص مد نظر باشد آنگاه 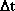 تا حد امكان كوچك (و نه صفر) انتخاب میكنیم.
تا حد امكان كوچك (و نه صفر) انتخاب میكنیم.
با استفاده از نماد گذاریِ نیوتن میتوان تندی لحظهای را به عنوان مشتق معادله مكان - زمان در نظر گرفت.
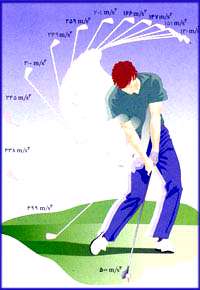
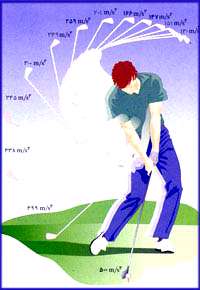
در شكل زیر شما مسیر نوك چوب گلف را مشاهده میكنید و L طول مسیر منحنی را از نقطه آغازین (L=0 ) نشان میدهد.
در هر لحظه، آهنگ حركت نوك چوب گلف برابر خواهد بود با:
به همین نحو، وقتی خلبان فضاپیمای شاتل گزارش میدهد كه تندی 7/82km/h است، درواقع او در حال صحبت كردن از رابطه زیر در آن لحظه میباشد.
مشتق گیری وقتی مفید است كه ما با دقت خوبی وابستگی یك متغیّر به متغیّر دیگر را بدانیم. به عنوان مثال، هنگامی كه حركت راكت را بررسی میكنیم ممكن است معادله ریاضی حركت در اختیار باشد یا مسافت طی شده بر حسب زمان قابل محاسبه باشد بنابراین (L) به عنوان تابعی از t در اختیار است. حال با مشتق گیری از L(t) نسبت به t تندی لحظهای محاسبه میگردد.
اگر مایل باشید طرز كار سرعت سنج را مشاهده كنید، با ماه همراه باشید.
تندی سنج
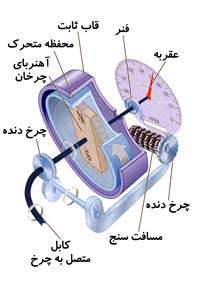
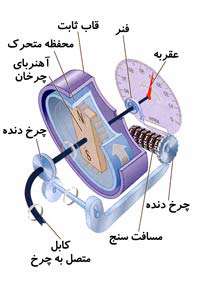
در شكل زیر نمای تندی سنج را مشاهده میكنید.
در تصویر زیر طرز كار تندی سنج را مشاهده میكنید. وقتی چرخ ماشین میچرخد، یك كابل ظریف و قابل انعطاف همزمان با آن به چرخش درمی آید. انتهای دیگر كابل به آهنربایی وصل است كه باعث چرخش آن میگردد.
چرخش آهن ربا باعث اعمال نیرو به قاب حلقوی میشود. ولی چرخش قاب توسط فنری محدود میگردد، به طوری كه موقعیت قاب متناسب با تندی می گردد. به قاب عقربهای وصل است كه میتواند تندی را نشان دهد.
مرکز یادگیری سایت تبیان - تهیه: محسنی
تنظیم: مریم فروزان کیا