محاسبات حركت پرتابی
در فصل قبل، حركت در راستای یك بعد را به‌كمك معادلات سینماتیكی تحلیل نمودیم. نكته كلیدی در تحلیل حركت دو بعدی این است كه حركت را به دو بخش یك بعدی تقسیم كنیم، سپس با تركیب آن ها پاسخ نهایی را به دست آوریم.
در اینجا ما فرآیندی را خواهیم آموخت كه در آن مسأله به چند مرحله و گام تقسیم می‌شود.
در شكل زیر روش حل حركت پرتابی را مشاهده می‌كنید.
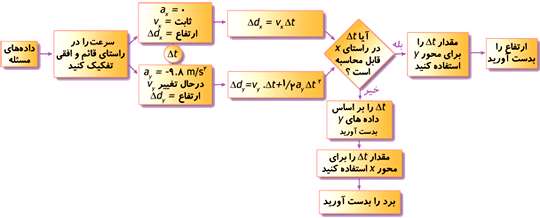
برای درک مطالب فوق به مثال زیر توجه نمایید.
شكل زیر هواپیمایی را نشان می‌دهد كه در ارتفاع ١٠٥٠m با تندی +115m/s به صورت افقی در حال پرواز است. جهت بالا و راست مثبت فرض می‌شود. بسته‌ای از هواپیما رها می‌شود و طی یك مسیر پرتابی سقوط می‌كند. با صرفه نظر كردن از مقاومت هوا، زمان لازم برای رسیدن بسته به زمین را حساب كنید.
راهنمایی:
زمان لازم برای رسیدن بسته به زمین معادل زمان لازم برای حركت بسته به اندازه ١٠٥٠m در راستای قائم می‌باشد. البته در هر حال بسته هم به راست و هم به پایین حركت می‌كند.
اما این دو حركت مستقل از هم روی می‌دهند. بنابراین ما توجّه مان را فقط به راستای عمودی معطوف می‌كنیم. بسته در لحظه جدا شدن از هواپیما هیچ تندی اوّلیه‌ایی در راستای قائم ندارد یعنی V0y=0 .
همچنین وقتی بسته به زمین می‌رسد، جا به جایی قائم بسته برابر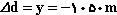 
خواهد بود. شتاب حركت در راستای قائم نیز ay=9/8m/s2 است.
این داده‌ها به شرح زیر خلاصه شده‌اند.
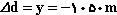
رابطه‌ایی كه این اطلاعات را در بر دارد عبارتست از:
حل:
از آنجا كه V0y=0 معادله به صورت زیر خواهد بود:
پس بر اساس رابطه فوق خواهیم داشت:
اگر مایل بودید این حركت را تصوّر كنید، به فیلم زیر توجّه كنید.
مرکز یادگیری سایت تبیان - تهیه: محسنی
تنظیم: مریم فروزان کیا
