طناب مرتعش

حالت اصلی ارتعاشی یک طناب کشیده شده طبق رابطه L=λ/2 به صورت دو برابر بودن طول موج نسبت به طول طناب تعریف می شود:

با استفاده از روابط پایه ای در فیزیک می توان رابطه سرعت موج، طول موج و فرکانس را به دست آورد:
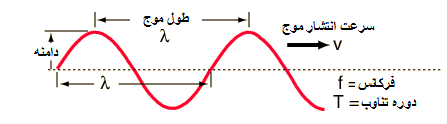
که زمان لازم برای انجام کامل یک نوسان را با T نشان داده ایم.
حال با استفاده از رابطه f=١/T رابطه استاندارد امواج را به دست می آوریم:

با استفاده از رابطه اخیر و L=λ/2 داریم:




این تصویر یک موج ایستاده تشدیدی روی طناب را نشان می دهد. توسط یک ارتعاش کننده در ١٢٠ هرتز می توان این موج را تولید کرد.
 |  |  |
هارمونیک ها:
در بالا اشاره شد که یک طناب ایده آل مرتعش با فرمانس اصلی و تمام هارمونیک های آن فرکانس ارتعاش خواهد کرد. مکان گره ها و شکم ها دقیقا مخالف حالت ستون هوا خواهد بود:
 مکان گره ها و شکم ها در یک طناب مرتعش |
 مکان گره ها و شکم ها در ستون هوا |
و هارمونیک ها مضرب های صحیحی هستند.

















