مثلث

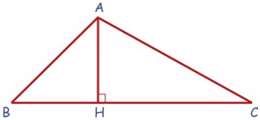
ارتفاع:

خطی که از یک رأس بر ضلع مقابل یا امتداد آن عمود می شود. (AH)

میانه:

خطی که از رأس به وسط ضلع مقابل وصل  می شود. (AM)

نیمساز:

خطی که زاویه را به دو قسمت مساوی تقسیم می کند. (AD)

عمود منصف:

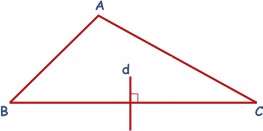
خطی که به وسط ضلع هر مثلث عمود شود. (خط d عمود منصف BC است)

انواع مثلث:

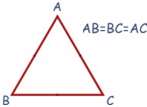
الف) مثلث متساوی الاضلاع:

مثلثی که سه ضلع آن با هم برابرند.

ب) مثلث متساوی الساقین:

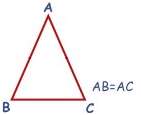
مثلثی که دو ضلع آن با هم برابرند.

ج) مثلث قائم الزاویه:

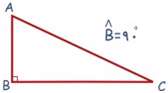
مثلثی که یک زاویه قائمه داشته باشد.

د) مثلث غیر مشخص:

مثلثی که هیچ یک از خصوصیات بالا را نداشته باشد.

 تساوی مثلث ها:

دو مثلث که بر هم منطبق شوند و کاملاً یکدیگر را بپوشانند با هم مساوی هستند. ما با داشتن فقط سه جزء از اجزای اصلی دو مثلث می توانیم ثابت کنیم که دو مثلث با هم برابرند. این سه جزء اصلی باید به صورت زیر باشد:

حالت دوم: دو زاویه و ضلع بین آن ها (ز ض ز)

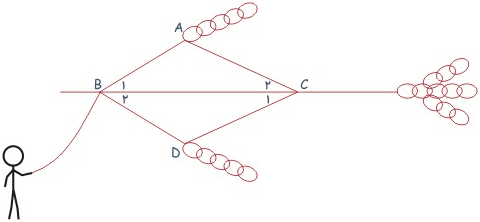
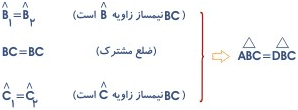
این دو مثلث بنابر حالت دو زباویه و ضلع (ز ض ز) با هم مساویند .

تساوی اجزای متناظر:

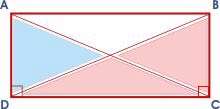
دو مثلث ABC و ADC را در نظر بگیرید. ابتدا ثابت می کنیم که این دو مثلث با هم برابرند، سپس به کمک تساوی سایر اجزای متناظر نشان می دهیم که AC= BD

پایگاه المپیاد ریاضی

مرکز یادگیری سایت تبیان - تنظیم: یگانه داودی