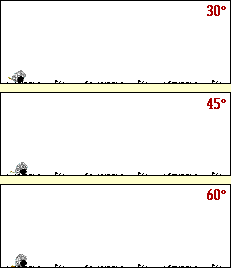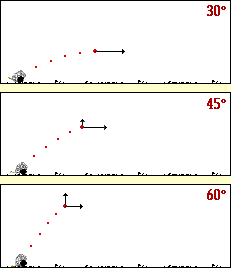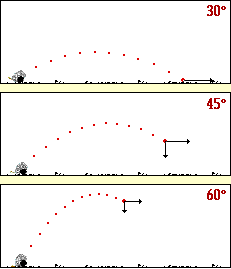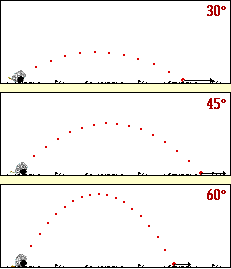
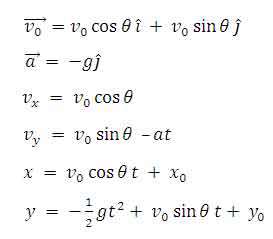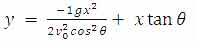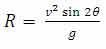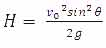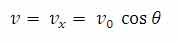بررسی حرکت دو بعدی

حرکت در دو بعد یکی از عام ترین حرکت هایی است که به طور روز مره با آن مواجه می شویم. حرکت یک اتومبیل در یک پیچ و یا حرکت یک گلوله پس از شلیک و یا رها شدن یک تیر از کمان از نمونه مثال هایی است که می توان از حرکت در دو بعد نام برد.

به طور کلی، حرکت در دو بعد ترکیبی از دو حرکت یک بعدی در دو راستای متفاوت  x و y می باشد. در این جا می خواهیم با صرف نظر کردن از نیروی اصطکاک فضایی که متحرک در آن حرکت می کند، را بررسی می کنیم.

حرکت پرتابه از دو نوع حرکت در راستای افقی و عمودی تشکیل شده است:

1 ) حرکت افقی حرکتی با شتاب صفر و با سرعت ثابت می باشد.

2 ) حرکت عمودی حرکتی با شتاب  g -  و در راستای عمودی است.

با توجه به شکل زیر می توانیم بردار سرعت و شتاب را به صورت زیر بنویسیم:

دقت داشته باشید که بردار رسم شده، بردار سرعت اولیه می باشد و زاویه نمایش داده شده، زاویه پرتاب اولیه می باشد، آن گاه خواهیم داشت :

معادله x ، معادله مکان بر حسب زمان پرتابه در راستای افقی می باشد و معادله y ، مکان متحرک در زمان های مختلف می باشد، در معادله x، مقدار t را به دست آورید و مقدار به دست آمده را در معادله y قرار دهید. مبدأ مکان و زمان را روی صفر قرار دهید (t₀=0   و x₀ = y₀ = 0)

معادله y بر حسب x به صورت یک منحنی سهمی خواهد بود که تقعر منفی دارد.

برد پرتابه

مقدار بیشینه فاصله جسم از نقطه پرتاب را برد پرتابه می گویند و با R نمایش می دهند، اگر  متحرک در طی مسیر، در یک سطح هم تراز برگردد، می توان با صفر قرار دادن مقدار y در معادله فوق مقدار R را به صورت زیر به دست آورد:

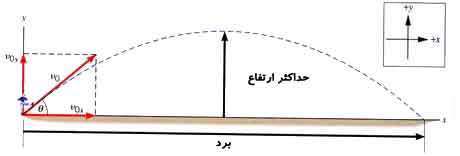
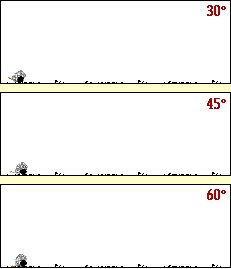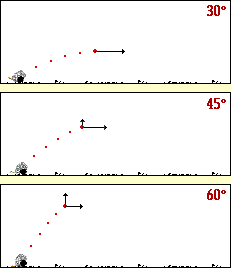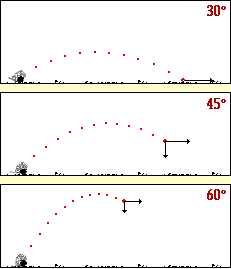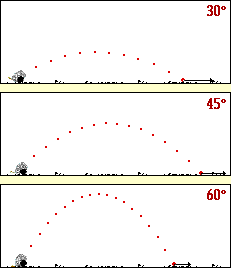
با توجه به شکل زیر آیا می توانید حدس بزنید که برد پرتابه تحت چه زاویه ای مقدار برد پرتابه بیشینه می شود؟

برای بررسی حدستان، می توانید به این شیوه عمل نمایید: تابع سینوس، تابعی است که برد آن در بازه [1 , 1- ] ، قرار دارد، با توجه به فرمول برد پرتابه، وقتی این مقدار بیشینه می شود که مقدار تابع سینوس یک شود، و این موقعیت وقتی روی می دهد که زاویه اولیه پرتاب 45 درجه باشد.