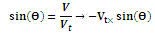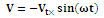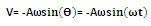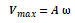سرعت
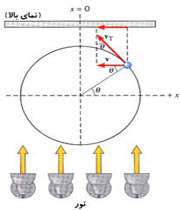
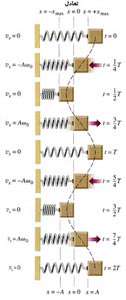
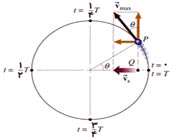
تاكنون موقعیت سایه توپِ در حال حركتِ یكنواختِ دایروی را بررسی كرده ایم. اما ما می توانیم ازدایره ای بودن حركت استفاده كنیم و به وسیله آن سرعت سایه را به دست آوریم.
به سرعت مماسی توپ ( Vt) روی دایره مرجع دواّر فكر كنید.
همان طور كه در شكل فوق ملاحظه می‌كنید سرعت Vt در راستای افقی دارای مؤلفه V می‌باشد. مقدار V را می توان به كمك روابط مثلثاتی به دست آورد.
البته از قبل می‌دانیم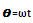 
،پس داریم:
علامت منفی در رابطه فوق به واسطه این است كه مؤلفه V سرعت به سمت چپ محور X می‌باشد.
امّا از قبل می‌دانیم كه سرعت مماسی Vt با شعاع (r) و سرعتِ زاویه‌ای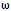 
رابطه دارد. به طوری‌كه داریم :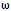* Vt= r و از آن جا كه در حركت فوق شعاع با A نشان داده شده است، بنابراین می توانیم بنویسیم: 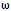*Vt = A
پس سرعت نوسان‌گر در حركتِ هماهنگِ ساده از رابطه زیر به دست می‌آید:
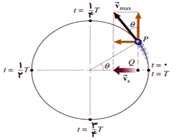
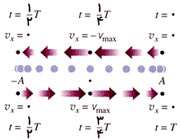
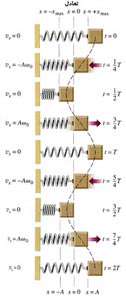
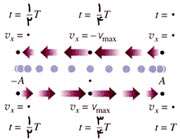
همان طور كه می‌بینید مقدار سرعت ثابت نبوده و به مرور زمان بین مقادیر مشخصی تغییر می کند.
در لحظاتی كه جهت حركت نوسان گر تغییر می‌كند، سرعت توپ چه قدر است؟
در چه لحظاتی سرعت نوسان گر توپ به حداكثر خود می‌رسد؟
سرعت نوسان‌گر بین چه مقادیری تغییر می‌كند؟
از آن جا که تابع سرعت از نوع سینوسی است و از طرفی سینوس بین 1+و 1- تغییر می كند، بنابراین حداكثر سرعت نوسان گر برابر است با:
پس برای تعیین حداكثر سرعت نوسان گر به هر دو مقدار دامنه نوسان (A) و بسامدِ زاویه ای 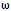نیاز داریم.
گروه مدرسه اینترنتی سایت تبیان - تهیه: محسنی
تنظیم: سمیرا بادامستانی
