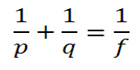محل و مشخصات تصویر در عدسی محدب
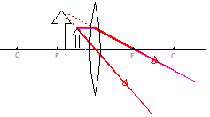
اكنون می خواهیم موقعیت تصویر در عدسی را برای حالت های مختلف بررسی نماییم. برای به دست آوردن موقعیت تصویر از دو پرتوی اصلی استفاده می كنیم.
به مدل سازی زیر توجه كنید و موقعیت تصویر را در هر حالت به دقت مشاهده نمائید.
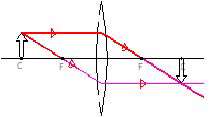
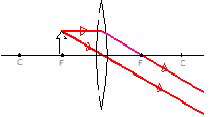
| شئ : خارج از مركز تصویر : بین مركز و كانون كوچكتر وارون حقیقی | |
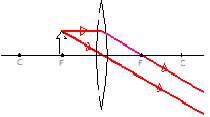
| شئ : روی مركز تصویر : روی مركز هم اندازه وارون حقیقی | |
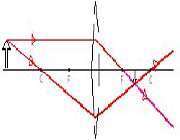
| شئ : بین مركز و كانون تصویر : خارج از مركز بزرگتر وارون حقیقی | |
|
شئ : روی كانون تصویر : تشكیل نمی شود ( واقع در بینهایت ) | |
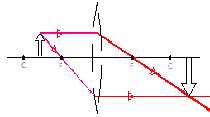
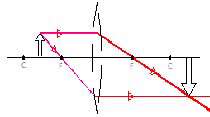
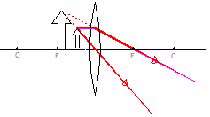
| شئ : بین عدسی و كانون تصویر : پشت عدسی بزرگتر مستقیم مجازی |
در صورتی كه فاصله شئ تا عدسی را با علامت ( p ) و فاصله تصویر تا عدسی را با علامت ( q ) و فاصله كانونی عدسی را با علامت ( f ) مشخص كنیم ، رابطه زیر بین این كمیت ها بر قرار است:
در مدل سازی زیر فاصله كانونی عدسیcm 10 است. شما می توانید موقعیت شئ را تغییر دهید، برای این منظور روی object position تقه زده و آن را جابجا كنید.
به دقت به معادله عدسی توجه كنید.
شما مشاهده می كنید اعداد فاصله q طوری متناظر با p تغییر می كند كه معادله عدسی همیشه برقرار باشد.
سوال : شی در چه موقعیت هایی قرار گیردتا q مقدار منفی داشته باشد؟
آیا معادله عدسی به نوع عدسی محدب (دوكاو، كاوتخت و هلالی كاو) بستگی دارد؟
برای پاسخ به این سوال بر روی (Bi_convex lens )تقه زده و حالت های مختلف را امتحان كنید.
برای علاقمندان به دانستن بیشتر !
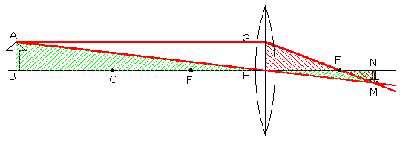
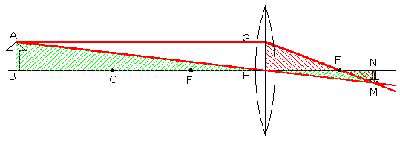
در این شكل دو مثلث GHF و MNF با یكدیگر متشابه اند . از این تشابه تساوی (2) نتیجه می شود.
از آنجا كه AB = GH ، تساوی (2) به صورت زیر در می آید:
با تركیب تساوی های (1) و (3) ، تساوی (4) حاصل می شود.
قدم بعدی آن است كه به جای هر یك از چهار پاره خط شركت كننده در رابطه (4) ، مقدار آنها را بر حسب p (فاصله شئ تا عدسی) ، q (فاصله تصویر تا عدسی) وf (فاصله كانونی یا نصف شعاع عدسی) قرار دهیم.
با دقت در شكل و ناچیز فرض كردن اثر انحنای عدسی، چهار رابطه زیر به دست می آید:
BH = p
NH = q
HF = f
NF = NH -HF = q -f
بنابرین ، تساوی (4) به صورت زیر در می آید:
(p / q = f / ( q -f
با ضرب طرفین و وسطین تساوی فوق ، تساوی زیر به دست می آید:
با ساده كردن ، رابطه زیر به دست می آید:
با تقسیم دو طرف این تساوی بر pqf ، تساوی مهم زیر به دست می آید:
شما در بالا با چگونگی بدست آوردن معادله عدسی آشنا شدید. خوب است صحت این معادله را برای موقعیت های مختلف شی و مقادیر مختلف فاصله كنونی و ارتفاع شئ بررسی كنیم.
به مدل سازی زیر توجه كنید.
در این مدل سازی شما می توانید با Object poeition موقعیت شی و با Focal lenght فاصله كانونی و با object height ارتفاع شئ و با Principle plane فاصله تیغه متوازی السطوح وسط عدسی را تغییر دهید.
سعی كنید هر كدام را جداگانه تغییر دهید و همزمان به صحت معادله عدسی توجه نمائید.
به نظر شما آیا فاصله تیغه متوازی السطوح وسط عدسی اثری در معادلات عدسی دارد؟
گروه مدرسه اینترنتی سایت تبیان - تهیه: محسنی
تنظیم: سمیرا بادامستانی