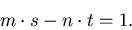امنیت اویلری 
حتماً این سوال برایتان پیش آمده است که چه طور میتوان کلیدهایی با مشخصات شرح داده شده، ساخت. یکی از روش های انجام این کار الگوریتم RSA است که نامش را از حروف اول نام سازندگانش میگیرد. مبنای اصلی این الگوریتم قضیه ی تقریباً ساده ای در نظریه ی اعداد مقدماتی است که به قضیه ی اویلر معروف است. اما جزئیات ساختن کلیدها: - ابتدا دو عدد اول نسبتاً بزرگ مثل p و q را در نظر میگیریم.
- عددی مانند k که نسبت به (p-1)(q-1) اول و هم چنین کوچک تر از N = p.q باشد، پیدا میکنیم.
- عددی مانند s را می یابیم به طوری که با قیمانده ی تقسیم k.s بر N=p.q ، یک باشد وs < N.
جفت (N, k) را به عنوان کلید عمومی منتشر میکنیم و جفت(N, s) را به عنوان کلید خصوصی نگه میداریم. کلیدها چگونه محاسبه میشوند؟ همان طور که بیان شد روشها ی محاسباتی خوبی برای تست اول بودن و تولید اعداد اول وجود دارد که به کمک انها p و q را انتخاب میکنیم. پیدا کردن k ساده است و انتخاب های زیادی وجود دارد، مثلاً می توان هر عدد اول کوچک تر ازN را به کار برد. می دانیم اگر m و n نسبت به هم اول باشند، آن گاه به کمک الگوریتم اقلیدس میتوانیم اعدادs وt را بیابیم، به طوری که: 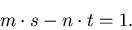 اگر الگوریتم اقلیدس را روی k و (p-1)(q-1) اعمال کنیم، خواهیم داشت: 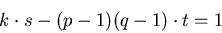
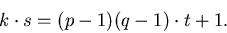
به این شکل می توانیم s را از رابطه ی بالا محاسبه کنیم. توجه کنید شرطی را که برای s گذاشتیم، به این ترتیب برآورده میشود: 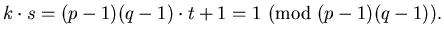
| برای فرستادن پیام، طرف مقابل باید ابتدا پیام را به یک عدد کوچک تر ازN مثل a ( یا در صورت طولانی بودن به چند عدد با همین شرط) تبدیل کند. سپس a را به توان k برساند و باقیمانده ی تقسیم 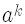 برN را مخابره کند. برN را مخابره کند. 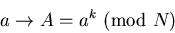
اگر s را مطابق روش گفته شده انتخاب کرده باشیم، همان طور که در کادر بعدی خواهیم دید، داریم: 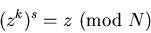
یعنی برای باز کردن رمز کافی است عدد رسیده (مثلاً A) را به توان s برسانیم و باقیمانده ی تقسیم آن به N را محاسبه کنیم: 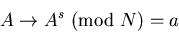
مشاهده می کنید که هر کس با دانستن k یا کلید عمومی میتواند برای شما پیغام بفرستد. اما بازگشایی رمز، مشروط به دانستن s و در نتیجه دانستن عوامل اول N یعنی p و q است. یعنی برای بازگشایی رمز باید یک عدد بزرگ با عوامل اول بزرگ را تجزیه کنیم. هر چه این عدد بزگ تر باشد، این تجزیه همان طور که در بخش های قبل گفتیم ناممکن تر است و اطلاعات ما امن تر خواهند بود. در کاربردهای عملی از اعدادی با حدود 100 رقم و بیش تر استفاده میکنند. چرا این روش، عمل می کند؟ همان طور که در ابتدای مطلب بیان شد این روش بر اساس قضیه ی اویلر ساخته شده است: قضیه ی اویلر: اگر z و N نسبت به هم اول باشند، آن گاه :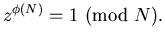 که در آن (N) 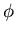 ( مشهور به تابع فی اویلر)، تعداد اعداد کوچک تر ازN است که نسبت به N اول هستند. ( مشهور به تابع فی اویلر)، تعداد اعداد کوچک تر ازN است که نسبت به N اول هستند. با دانستن این قضیه و توجه به این نکته که اگر N = p.q آن گاه (N)=(p-1)(q-1) 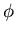 است و اگر k وs همان کلیدها باشند و z صورت اولیه پیام باشد، داریم: است و اگر k وs همان کلیدها باشند و z صورت اولیه پیام باشد، داریم: 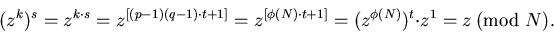
و از آن جا که z کوچک تر ازN و مثبت است، تساوی آخر به پیمانه ی N به تساوی معمولی تبدیل میشود. | |