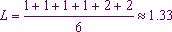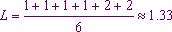این دنیای کوچک
حتماً تا حالا شنیدید که ؛ "عجب دنیای کوچیکیه". یا اینکه "کوه به کوه نمی رسه ولی آدم به آدم میرسه". یا حتی اینکه "گذر پوست به دباغ خونه میافتد" و ... همهی این ضرب المثلها بر کوچکی دنیا و نزدیکی آدمهای آن به هم دلالت دارند.
توی این مقاله میخواهیم ببینیم این دنیا واقعاً کوچک است یا آیا اصلاً میشود کوچکی یا بزرگی دنیا را اندازه گرفت؟ آیا واقعاً با اینکه کوه به کوه نمی رسه، آدم به آدم میرسه؟!
در سالهای اخیر، تعداد زیادی از فیزیکدانها و کارشناسان و محققان علوم کامپیوتر و حتی تعدادی از ریاضیدانها، مشغول بررسی خصوصیات شبکه های مختلف و انواع ارتباطات و ویژگیهای اتصالات آنها شده اند.
ابتدا تعریف چند اصطلاح:
رأس: در دیدگاه شبکه ای (Network) به اعضای اصلی یک مجموعه که هدف، بررسی ارتباطات این اعضا است، رأس گفته میشود.
مثلاً در شبکه راههای یک کشور، شهرها رئوس شبکه هستند. یا در شبکه های اینترنتی، هر پایگاه یک رأس از شبکه است. در شبکه های اجتماعی، معمولاً انسانها نقش رئوس را بازی میکنند و در شبکه های اقتصادی شرکتها و مؤسسات اقتصادی رئوس شبکه هستند.
یالها یا اتصالها: یالها یا اتصالها بیانگر وجود رابطه ای بین دو رأس از شبکه هستند. به عبارتی، هر گاه بین دو رأس از یک شبکه، یک یال یا اتصال برقرار باشد به این معنی است که این دو رأس، به هم مرتبط اند. واضح است که وجود یال بستگی به تعریف ما از رابطهی بین دو رأس دارد. مثلاً در یک شبکهی راههای یک کشور، وجود یال به معنی وجود جاده، در شبکهی پایگاههای اینترنتی به معنای وجود لینک، در یک شبکهی اجتماعی، وجود رابطهی دوستی و یا در شبکه های اقتصادی وجود شراکت تجاری و ... میباشد.می بینیم که با این تعریف های ساده، یک مجموعهی پیچیده از اعضای مختلف با ارتباطهای پیچیده را میتوان به مجموعه ای از رئوس و یالها ساده کرد. معمولاً در نمایش شبکهها از نقاط به عنوان رئوس و از خطوط متصل کننده نقاط به عنوان یال استفاده میشود.
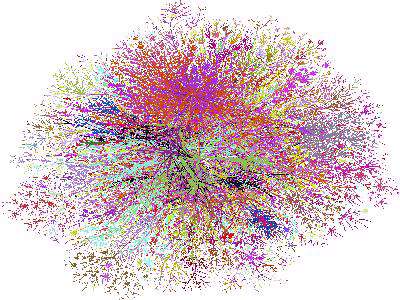
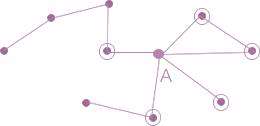
شکل زیر بخشی از نمایش شبکه W.W.W (شبکه وب سایتهای جهانی) است.
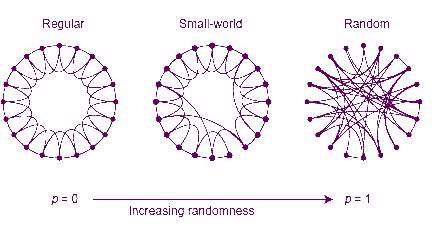
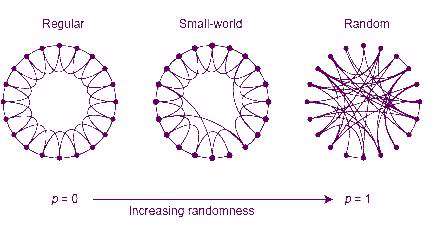
شبکه های منظم (Regular)
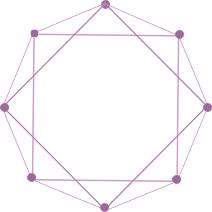
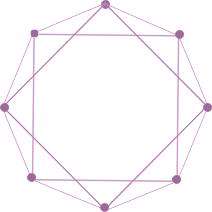
شبکه های منظم شبکه هایی هستند که یالها و رأسهای آن به طور منظم و معمولاً متقارن در کنار هم قرار گرفته اند. به طوری که نمایش آنها معمولاً به شکل چند ضلعی های منتظم که قطرهای خاصی از آنها رسم شده اند، می باشد. به طور مثال شکل زیر یک شبکهی منتظم شامل 8 رأس و 16 یال است. در این شبکه هر عضو با 4 عضو دیگر در ارتباط است. و موقعیت تمامی اعضا، کاملاً یکسان است.
معمولاً در دنیای واقعی به ندرت با شبکه های منظم برخورد می کنیم.
شبکههای تصادفی (Random)
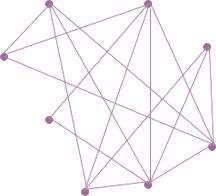
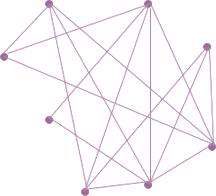
شبکه های تصادفی شبکه هایی هستند که یالهای موجود در آنها به صورت کاملاً تصادفی، رئوس را به هم متصل کرده اند و هیچ نظم و قانونی بر اینکه کدام دو رأس به هم متصل شوند، وجود ندارد. به طور مثال شکل زیر نمایشی از یک شبکهی تصادفی است که 8 رأس و 16 یال دارد.
معمولاً شبکه های تصادفی تحت شرایطی که بی نظمی حاکم به سیستم زیاد است شکل میگیرند.
حال به دو تعریف مفید میپردازیم:
میانگین طول مسیر(mean path length)-(L)
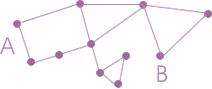
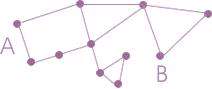
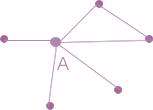
طول مسیر، تعداد یالهایی است که باید طی شود تا از یک رأس مشخص به رأس مشخص دیگری رسید. مثلاً در شکل زیر طول مسیر بین رأس A و B برابر 4 است. البته اگر چند مسیر بین دو رأس مورد نظر وجود داشته باشد، طول کوتاهترین مسیر به عنوان طول مسیر شناخته میشود.
حال اگر روی کل طول مسیرهای ممکن در یک شبکه، میانگین بگیریم، به میانگین طول مسیر دست پیدا میکنیم. مثلاً در شبکه شکل زیر میانگین طول مسیر 1.33 است.
زیرا طول مسیر بین 1و2- 2و4 - 4و3 برابر 1 است و طول مسیر بین 1و4 - 4و3 برابر 2 است.
به زبان دیگر میانگین طول مسیر بیان میکند به طور میانگین فاصله بین 2 رأس در شبکه چقدر است یا اینکه به طور میانگین 2 رأس در شبکه با چند واسطه با هم در ارتباطند.
ضریب خوشیدگی (Clustering coeficent)-(C)
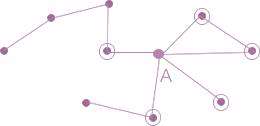
ضریب خوشیدگی یا ضریب خوشه ای شدن بر روی یک شبکه به صورت زیر تعریف میشود. یک رأس خاص از شبکه را در نظر بگیرید. فرض کنید تعداد همسایه های این رأس یعنی رأسهایی که با آن بدون واسطه ارتباط دارند n باشد.
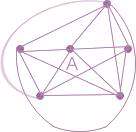
رأس A در شبکه شکل زیر:
n=5
اگر فقط به مجموعه A و همسایهی آن نگاه کنیم: تعداد کل یالهای موجود در این زیر شبکه 6 است.
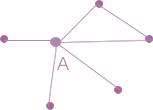
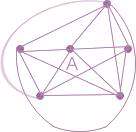
در حالیکه اگر تمام همسایه های A با هم ارتباط داشتند یعنی مثل شکل زیر:
تعداد یالها به 15 افزایش مییافت.
( به شبکه ای که تمام یالهای ممکن در آن وجود داشته باشد شبکه کاملاً متصل full connected میگویند.)
اما از این 15 یال ممکن که 10 تای آنها مربوط به اتصال همسایه های A به یکدیگر است، تنها 5 یال که فقط یکی از آنها مربوط به اتصال همسایه های A هستند موجود است. به نسبت تعداد یالها (اتصالات) موجود بین همسایه های یک رأس با هم، به تعداد یالهای ممکن ضریب خوشیدگی یا خوشه ای شدن رأس مورد نظر میگویند.
به عبارتی هر چه همسایه های یک رأس نیز با یکدیگر همسایه باشند، این ضریب افزایش مییابد. اگر ضریب خوشیدگی تمامی رئوس را میانگین گیری کنیم به ضریب خوشیدگی کل میرسیم. واضح است که بیشترین مقدار این ضریب مربوط به شبکهی کاملاً متصل است.
که ضریب خوشیدگی کل آن برابر یک است. زیرا همهی همسایه های یک رأس با هم نیز همسایه اند. کمی به این تعاریف و مثالها فکر کنید تا به این سئوال که چقدر دنیا کوچک است جواب دهیم!
دوباره به شبکه های منظم (regular) و تصادفی (random) برمی گردیم. و در مورد میانگین طول مسیر و ضریب خوشیدگی آنها بحث میکنیم.
ویژگی خاص شبکه های منظم این است که این شبکهها ضریب خوشیدگی(C) زیاد و نیز میانگین طول مسیر(L) بزرگی دارند. یعنی هم تعداد همسایه های یک رأس که با هم همسایه اند زیاد است و هم فاصلهی دو رأس به طور میانگین. این نتایج با استفاده از شبیه سازیهای ساده ای که مقدار L و C را برای شبکه های منظم مختلف اندازه گیری میکند، بدست آمده است.
از طرفی شبکه های تصادفی ضریب خوشیدگی کم و میانگین طول مسیر کوتاه دارند.
یعنی معمولاً رئوس فاصله کمی با هم دارند و با واسطه های کم میتوان از یکی از رئوس به رأس دیگری رسید.
پس از بررسی " شبکه های دنیای کوچک " میتوانیم توضیحی برای خصوصیات بالا ارائه کنیم و بفهمیم اساس این ویژگیها چیست.
شبکه های دنیای کوچک
در واقع شبکه های دنیای کوچک حالتی بین شبکه های منظم و شبکه های تصادفی است.فرض کنید شبکهی منظم با n رأس در اختیار داریم که بصورت زیر نمایش داده شده است:
برای تبدیل این شبکه به یک شبکهی تصادفی از روش زیر که باز اتصال (Rewiring) نام دارد، استفاده میکنیم:
یک رأس را در نظر میگیریم، اگر این رأس K یال داشته باشد (در مثال بالا K = 4) هر یال را با احتمالP از بین برده و بهجای آن، یک یال از رأس مذکور به یک رأس دلخواه که بهصورت تصادفی از بین رئوس دیگر انتخاب شده است، ایجاد میکنیم. یعنی با احتمالP به جای هر یال موجود یک یال تصادفی جایگزین میکنیم.
هر چهP بزرگتر باشد (توجه کنید کهP عددی بین صفر و یک است)
احتمال وقوع یک باز اتصال بیشتر است. اگرP صفر باشد یال مذکور به همان صورت قبلی باقی میماند.
پس از اینکه برای یک رأس این کار را انجام دادیم به سراغ رأس بعدی میرویم و همین طور تک تک یالهای همه رأسها را با احتمالP، باز اتصال میدهیم. واضح است که اگرP=1 باشد به یک شبکهی کاملاً تصادفی میرسیم و اگرP=0 باشد شبکهی منظم باقی میماند. میتوانید امتحان کنید:
و در موردP های بین صفر و یک در اصل یک شبکهی منظم، نیمه تصادفی داریم.
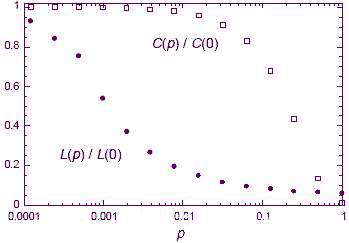
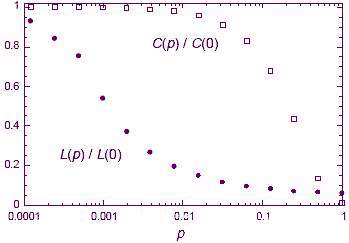
شکل زیر تغییرات L و C را بر حسبP نشان میدهد.
همانطور که میبینید شبکهی منظم هم L ( میانگین طول مسیر) و هم C (ضریب خوشه ای شدن) بزرگ دارد و شبکهی تصادفی هم L و C کوچک اند. اما شبکه های دنیای کوچک همانطور که قبلاً گفتیم دارای مقادیری بین این دو می باشند، یعنی شبکه های بازسازی شده با P تقریباً برابر 0.01 است که میبینید L کوچک و C بزرگ دارند!
یعنی در این شبکهها علاوه بر اینکه فاصلهی دو رأس کم است بلکه همسایهها نیز همدیگر را میشناسند. یاد خودتان نیفتادید؟
مهمترین مثال شبکهی دنیای کوچک، مثال روابط اجتماعی است. فرض کنید شبکه ای داریم که رئوس آن انسانها و اتصالها رابطهی دوستی باشد. دو رأس را دوست مینامیم اگر همدیگر را با نام کوچک صدا بزنند. یعنی هر دو آدمی که آنقدر صمیمی باشند که یکدیگر را با نام کوچک صدا بزنند با یک یال به هم متصل میشوند. به سادگی میتوان نشان داد این شبکه، شبکهی دنیای کوچک خواهد بود. میانگین طول مسیر در این شبکه در حدود 6 است!!!
یعنی هر دو آدمی در دنیا را در نظر بگیرید، به طور میانگین با 6 واسطه یعنی با 6 دوست صمیمی به هم متصل میشوند.
این است که میگویند که دنیا کوچک است یا اینکه آدمها به هم میرسند. تصور کنید شما و یک قصاب اوگاندایی فقط با چیزی در حدود 6 یا 7 وسطه با هم دوستید!
همچنین ضریب خوشیدگی نیز در مورد این شبکهها بسیار بالاست، حتماً شما هم دیده اید که معمولاً دوستانتان نیز با هم دوست هستند. و دوست مشترک بین شما و دوستانتان زیاد است. یا به عبارتی آدمها در این شبکه، دسته دسته اند و به خوشه هایی مجزا تبدیل شده اند که گاه با یک میانبر یک خوشه به خوشهی دیگری وصل میشود.
راز کوچک بودن L در شبکه های تصادفی هم همین است. در اصل نقش اصلی را میانبرها ( اتصالات جدید بلند که از یک سمت شبکه به سمت دیگر میروند) به عهده دارند، بررسی خصوصیات شبکه های دنیای کوچک بسیار مفید و پر کاربرد است.
کدام نوع از شبکه های سلولهای عصبی، بهترین یادگیری را دارند؟ شاید جالب باشد که بدانید در شبکه های دنیای کوچک از سلولهای عصبی یادگیری بسیار سریع تر از شبکه های منظم انجام میگیرد. در مغز ما هم اتفاقاً شبکهی سلول های عصبی از نوع شبکه های دنیای کوچک اند!!!
به نظر شما با نظارت بیشتر بر کدام سایتها میتوان از انتشار یک ویروس در کل شبکهی اینترنت جلوگیری کرد؟؟
نویسنده:طاها یاسری